In diesem Artikel möchte ich etwas über die stille Heldin der Kommunikation reden.
Die Verschlüsselung.
Diese stellt sicher, dass Nachrichten nur von den Personen gelesen werden können, die diese lesen sollen.

Ich weiß nicht, wie es dem Rest der Menschheit geht, aber ich fühle mich wohler, wenn ich im Glauben bin, dass meine WhatsApp-Nachrichten bzw. meine E-Mails nur von dem Empfänger und mir gelesen werden können. Nicht dass sich so ein aufregendes Leben hätte, aber es lässt mich doch besser einschlafen in der Nacht.

Um uns den heutigen Verschlüsselungstechniken zu nähern, lasst uns zunächst einen kurzen Ausflug über die Techniken der letzten Jahrhunderte machen.

Eine kurze Geschichte der Verschlüsselung

Skytale

Wahrscheinlich ist die erste Verschlüsselung wesentlich älter, jedoch will ich die erste Station bei der Skytale Chiffre machen. Diese Technik wurde bereits vor 2500 Jahren in Sparta eingesetzt um Nachrichten an Generäle auf dem Schlachtfeld zu übermitteln.
Der Name Skytale kommt dabei aus dem Altgriechischem und bedeutet so viel wie “Stock” oder auch “Stab”. Es wurde ein Stab genommen und in zwei Hälften getrennt. Die eine erste Hälfte bekam nun der Sender, die zweite der Empfänger. Sollte nun eine Nachricht übermittelt werden, wurde ein Streifen Leder um den Stab gewickelt. Die Nachricht konnte nun auf eine Seite des Stabs geschrieben werden. Der Rest des Streifens wurde anschließend mit zufällig gewählten Buchstaben aufgefüllt.

Auf dem obigen Bild ist eine Skytale abgebildet. Die entschlüsselte Nachricht lautet: “Karl ist der Verräter”. Wenn jedoch der Bote überfallen wird, kann nur das Lederband ohne den Stab sichergestellt werden. Die Botschaft, die auf dem Lederband zu lesen ist, ist: “KSVEJSIDWGATETOPWENQRDRENPKWETLERRNISFRBIRAB”.
Um dieses Wirrwarr an Buchstaben zu entschlüsseln, ist eben der Stab oder ein Stab mit demselben Durchmesser, der zum Schreiben benutzt wurde, zwingen erforderlich.

Ceasar Chiffre

Springen wir ein ca. 400 Jahre weiter. Nach Rom. Genauer gesagt zu Gaius Julius Cäsar. Es wird angenommen, dass Julius Caesar für seine militärische Korrespondenz die Caesar Chiffre verwendet hat. Wahrscheinlich hieß sie damals nicht so, aber sei es drum.
Die Caesar Chiffre zeichnet sich dadurch aus, dass jeder Buchstabe des Alphabets um eine bestimmte Anzahl nach rechts verschoben wird.

\[\begin{smallmatrix} A & B & C & D & E & F & G & H & I & J & K & L & M & N & O & P & Q & R & S & T & U & V & W & X & Y & Z \\ I & J & K & L & M & N & O & P & Q & R & S & T & U & V & W & X & Y & Z & A & B & C & D & E & F & G & H \end{smallmatrix}\]

In der obigen Abbildung wird eine Ceasar Chiffre mit dem Schlüssel $A = I$ dargestellt. Das bedeutet, dass jedes A durch ein I ersetzt wird, jedes B durch ein J, jedes C durch ein K und so weiter. Wenn nun die Nachricht “Auch du, mein Sohn” verschlüsselt versendet werden soll, lautet die verschlüsselte Nachricht “ICKPLCUMQVAWPV”.
Soll die Nachricht jetzt wieder entschlüsselt werden, kann die oben aufgestellte Tabelle von unten nach oben angewandt werden. Das bedeutet, man sucht den Buchstaben in der unteren Zeile und ersetzt ihn mit der oberen.
Der Schlüssel der Ceasar Chiffre ist also die Anzahl, um wie viel das Alphabet nach rechts verschoben wird.

Ein offensichtliches Problem dieses Verschlüsselungsverfahrens ist, dass es nur 25 Schlüssel gibt. Das bedeutet, man kann leicht alle möglichen Schlüssel ausprobieren, um so an die Nachricht zu kommen.

Zweiter Weltkrieg

Machen wir wieder einen deutlich größeren Zeitsprung. In die Zeit des Zweiten Weltkrieges.
Da alle Parteien davon ausgehen mussten, dass ihre Funksprüche abgehört werden, mussten diese verschlüsselt werden. Nazi-Deutschland benutzte für die Verschlüsselung die Enigma.
Die Enigma ähnelt vom Aussehen einer Schreibmaschine. Für jeden Buchstaben, den man eintippt, leuchtet ein anderer Buchstabe auf. So konnte man seine Nachricht eingeben und die Buchstaben, die dabei aufleuchten, ergaben die verschlüsselte Nachricht.
Den Vorgang der Verschlüsselung kann man sich ähnlich zur Ceasar-Chiffre vorstellen. Jedoch ist das Verschlüsselungsalphabet (unten) willkürlich angeordnet. Verantwortlich für die Anordnung des Verschlüsselungsalphabets waren zwei Bestandteile. Mehrere Walzen innerhalb der Maschine, sowie ein Steckbrett, welches für jeden Stecker zwei Buchstaben miteinander vertauscht hat. Wurde ein Buchstabe auf der Tastatur angeschlagen, haben sich die Walzen in eine neue Stellung gebracht und so das Verschlüsselungsalphabet wieder “durchgemischt”.

Um die Nachricht zu entschlüsseln, brauchte der Empfänger ebenfalls eine Enigma. Auch mussten die Walzenstellung sowie die Anordnung des Steckbrettes dieselbe sein, wie die, die zur Verschlüsselung benutzt worden ist. Anschließend konnten die einzelnen Buchstaben der verschlüsselten Nachricht eingegeben werden. Die Buchstaben, die dabei aufleuchteten, konnten zur ursprünglichen Nachricht zusammengesetzt werden.
Der Schlüssel, den die Enigma benutzte, war also die Stellung der Walzen und die Einstellung des Steckbretts. Diese wurden in einem Schlüsselbuch der Wehrmacht festgehalten.

Kalter Krieg

Auch die Spione, die auf beiden Seiten des Kalten Krieges tätig waren, mussten ihre Nachrichten verschlüsseln. Oft kam da das One-Time Pad bzw. das Einmalschlüssel-Verfahren zum Einsatz.
Voraussetzung war ein vorher ausgetauschter Schlüssel, der dieselbe Länge hat, wie die dazugehörige Nachricht.
Sehen wir uns dazu mal ein Beispiel an. Wir wollen folgenden Satz verschlüsseln:

\[\begin{smallmatrix} WIR &TREFFEN &UNS &MORGEN &UM &ZEHN &UHR \end{smallmatrix}\]

Um das Ganze zu vereinfachen, entfernen wir die Leerzeichen:

\[\begin{smallmatrix} WIRTREFFENUNSMORGENUMZEHNUHR \end{smallmatrix}\]

Als Schlüssel benutzen wir die folgende Zeichenkette:

\[\begin{smallmatrix} SFEIIWHBJQVUXFYHWYPRVQAMNSSG \end{smallmatrix}\]

Der Schlüssel wurde zufällig erstellt.
Um die Nachricht zu verschlüsseln, müssen wir zunächst zwei mathematische Hilfsmittel definieren. Zunächst die Funktion $f$, diese weißt jedem Buchstaben eine natürliche Zahl zu. Dabei ist A die 0, B die 1, C die 2, usw. bis Z = 25.
Anschließend noch der Modulo Operator. Hier müssen wir uns an die Grundschule erinnern. Der Modulo Operator ist nämlich nichts anderes wie die Division mit Rest.
Zum Beispiel ist $13 \text{ mod } 5 = 3$, da 3 hier den Rest angibt bei der Division $13/5$.
Wir verschlüsseln nun den ersten Buchstaben. Hierfür nehmen wir den ersten Buchstaben der Nachricht sowie den ersten Buchstaben des Schlüssels.

\((f(W) + f(S))\text{ mod }26\) Die 26 ergibt sich aus der Anzahl der Buchstaben in unserem Alphabet. Wenn wir nun die tatsächlichen Werte für $f(W)$ und $f(S)$ einsetzen, bekommen wir die Gleichung $(23 + 19) \text{ mod } 26 = 16$. Die Nummer 16 steht hierbei für den 17ten Buchstabe aus unserem Alphabet (da wir ja bei A mit 0 anfangen) und ist somit ein Q.

Machen wir das ganze für jeden Buchstaben unserer Nachricht, so bekommen wir diesen verschlüsselten Text:

\[\begin{smallmatrix} ONVBZAMGNDPHPRMYCCCLHPETAMZX \end{smallmatrix}\]

Diese verschlüsselte Nachricht kann nun ohne Bedenken übertragen werden.
Um die Mitteilung nun wieder lesen, bzw. entschlüsseln zu können, kann der Spion, der die Nachricht empfangen hat, (beinahe) dieselbe Methode wiederverwenden:

\[(f(W) - f(S))\text{ mod }26\]

Das Schöne an der Einmalverschlüsselung ist, dass sie unknackbar ist, solange der Schlüssel geheim und zufällig ist.

Und darin liegt auch schon der Knackpunkt von dieser und allen vorherigen Verschlüsselungsverfahren. Der Schlüssel muss geheim bleiben, aber beide Parteien müssen ihn kennen. Das bedeutet, dass der Schlüssel irgendwann ausgetauscht bzw. übertragen werden muss. Und hier könnte ein Angreifer zuschlagen und den Schlüssel auch in seinen Besitz bringen.

RSA-Verschlüsselung

Alle bis jetzt vorgestellten Verschlüsselungsverfahren sind sogenannte symmetrische Verschlüsselungsverfahren. Sie zeichnen sich dadurch aus, dass derselbe Schlüssel für die Ver- und Entschlüsselung der Nachricht verwendet wird.
Seit den 70ern gibt es eine weitaus genialere Methode, um Nachrichten zu verschlüsseln. Und das ganz ohne den Nachteil des gemeinsamen Schlüssels zu haben.
Die Rede ist von der sogenannten asymmetrischen Verschlüsselung, oder auch Public-Key-Verfahren.

In diesem Verfahren generiert jeder, der an einer verschlüsselten Konversation teilnehmen will, ein Schlüsselpaar. Dieses Paar besteht aus einem öffentlichen, für jeden sichtbaren, Schlüssel, und einem geheimen privaten Schlüssel.
Eine der ersten asymmetrischen Verschlüsselungssysteme war RSA aus dem Jahr 1977.

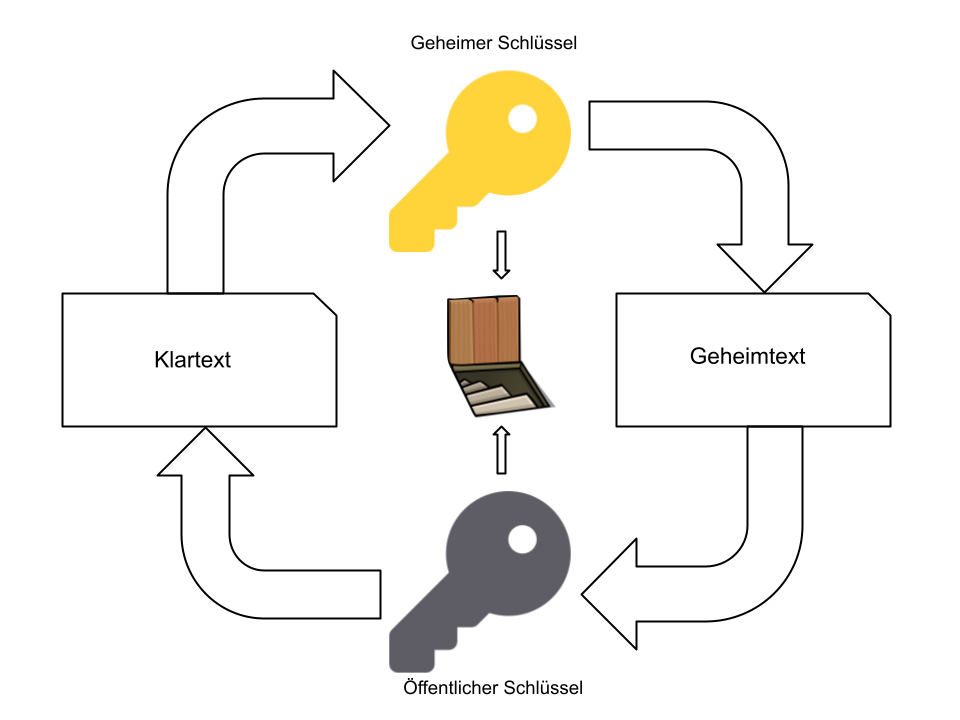
Wie in dem Schaubild zu sehen ist, werden beide Schlüssel für die Ver- und Entschlüsselung benötigt. Nehmen wir an, es gibt zwei Personen, die eine verschlüsselte Nachricht austauschen wollen. Wir nennen sie mal Adam und Berta. Jeder von ihnen besitzt ein eigenes, einzigartiges Schlüsselpaar (einen öffentlichen und einen privaten Schlüssel).
Den öffentlichen Schlüssel stellen beide Personen öffentlich bereit. Den privaten Schlüssel müssen beide geheim halten.

Jetzt will Adam eine Nachricht an Berta senden. Dabei verwendet Adam den öffentlichen Schlüssel von Berta um die Nachricht zu verschlüsseln. Die einzige Möglichkeit, die jetzt bleibt, um die Nachricht wieder lesen zu können, ist die Entschlüsselung des Textes mit dem privaten Schlüssel von Berta.

$\text{Nachricht}\xrightarrow[\text{öffentlicher Schlüssel}]{\text{Bertas}}\text{Geheimtext}\xrightarrow[\text{privater Schlüssel}]{\text{Bertas}}\text{Nachricht}$

Anders als bei den vorherigen Methoden, lässt sich die Nachricht nun nicht mehr mit demselben Schlüssel entschlüsseln, sondern nur noch mit einem zweiten Schlüssel.
Um das zu ermöglichen, müssen die beiden Schlüssel natürlich in einer Art von Beziehung stehen.
Leider müssen wir uns, um uns diese Beziehung genauer anzusehen, erst einmal ein paar mathematische Grundlagen ins Gedächtnis zurückrufen. Sollte man da grundlos zurückschrecken, kann gerne zum Kapitel Sicherheit gesprungen werden.

RSA Grundlagen

Teilermenge

Ein Teiler t einer Zahl n ist eine ganze Zahl, die durch n ohne Rest teilbar ist. Alle Teiler t der Zahl n ergeben die Teilermenge.
Beispiel:

\[12\quad\text{Teilermenge} = \{1, 2, 3, 4, 6, 12\}\\ 42\quad\text{Teilermenge} = \{1, 2, 3, 4, 6, 7, 14, 21, 42\}\\\]

Primzahl

Ein wichtiger Bestandteil der meisten asymmetrischen Verschlüsselungsverfahren sind die Primzahlen. Eine Primzahl ist eine Zahl, die nur durch 1 und sich selbst ohne Rest teilbar ist. Die Teilermenge einer Primzahl besteht also immer nur aus zwei Elementen. Beispielsweise ist 13 eine Primzahl.

Primfaktoren

Jede ganz Zahl n lässt sich durch Multiplikation von Primzahlen errechnen. Diese Primzahlen heißen dann Primfaktoren der Zahl n. Deswegen können die Primzahlen auch als Bausteine der natürlichen Zahlen betrachtet werden. Zwei kleine Beispiele:

\[42 = 2 * 3 * 7\\ 12 = 2 * 2 * 3\]

Diese Zerlegung in Primfaktoren, genannt Primfaktorzerlegung, ist einer der wesentlichen Tricks, welchen das RSA Verfahren sicher machen. Die Primfaktorzerlegung für sehr große Zahlen ist nämlich extrem schwierig zu berechnen.

Größter gemeinsamer Teiler

Der größte gemeinsame Teiler (ggT) von zwei Zahlen a, b ist der größte Teiler den a und b gemeinsam haben. Zum Beispiel ist der ggT von 12 und 42 ist die 6.

Teilerfremd

Zwei Zahlen a, b sind teilerfremd, wenn diese keinen gemeinsamen Teiler außer die 1 haben. Beispiel:

\[15\quad\text{Teilermenge} = \{1, 3, 5, 15\}\\ 22\quad\text{Teilermenge} = \{1, 2, 11\}\]

Das einzige Element, welches beide Teilermengen gemeinsam haben, ist die 1. Somit sind 15 und 22 teilerfremd zueinander. Im Übrigen wäre der größte gemeinsame Teiler von 15 und 22 damit auch die 1.

Eulersche $\phi$-Funktion

Die Eulersche $\phi$-Funktion $\phi(n)$ gibt an, wie viele ganze Zahlen, die kleiner als n sind, teilerfremd zu n sind.

\[\phi(12) = 4 \quad\{1, 5, 7, 11\}\]

Für 12 gibt es also 4 Zahlen, die kleiner als 12 und teilerfremd zu ihr sind. Nämlich die 1, 5, 7 und 11.
Die Eulersche $\phi$-Funktion ist für große Zahlen sehr schwer zu berechnen.
JEDOCH ist die Eulersche $\phi$-Funktion sehr leicht zu berechnen, wenn n eine Primzahl ist. Wir erinnern uns: jede Primzahl ist nur durch 1 und sich selbst teilbar. Das bedeutet, jede kleinere Zahl als n ist teilerfremd zu n.

\[\phi(7) = 6 \quad\{1, 2, 3, 4, 5, 6, 7\}\]

Um das allgemeiner für eine beliebige Primzahl p auszudrücken:

\[\phi(p) = p-1\]

Eine weitere Besonderheit von der Eulerschen $\phi$-Funktion ist, dass sie multiplikativ ist. Das bedeutet, dass \(\phi(a*b) = \phi(a) * \phi(b)\) ist.
Im RSA Algorithmus wird ausgenutzt, dass die Eulersche $\phi$-Funktion von einem Produkt aus Primzahlen p, q so umgeschrieben werden kann:

\[\phi(p*q) = \phi(p) * \phi(q) = (p-1)(q-1)\]

Multiplikatives Inverses

Das multiplikative Inverse einer natürlichen Zahl n wird oft $n^{-1}$ geschrieben. Wichtig beim multiplikativen Inversen ist, dass es multipliziert mit der Zahl n die 1 ergibt. Sprich $n * n^{-1} = 1$. Würden wir uns im Bereich der reellen Zahlen bewegen, wäre das multiplikative Inverse immer leicht zu berechnen, nämlich $\frac{1}{n}$.

Leider ist das bei den natürlichen, ganzen Zahlen nicht so einfach. Hier müssen wir das multiplikative Inverse innerhalb einer Gruppe $\mathbb{Z}_a$ bilden. Das heißt wir suchen das multiplikative Inverse für eine natürliche Zahl n für die Gruppe a.
Sprich: \((n*n^{-1}) \text{ mod } a\)
Ein Beispiel:
Das multiplikative Inverse für $n=5$ und $a = 6$ ist 5. Da $(5*5) \text{ mod } 6 = 1$.

Wir sollten ebenfalls beachten, dass nicht immer ein multiplikatives Inverses existiert. Zum Beispiel besitzt $n=2$ und $a=6$ kein multiplikatives Inverses. $2^{-1}$ existiert also nicht für $\text{mod }6$. Die Bedingung, dass es ein multiplikatives für $\text{mod } a$ gibt, ist, dass n und a teilerfremd sind. Es muss also gelten: $ggT(n, a) = 1$, sodass ein multiplikatives Inverses existieren kann.
Sollte n eine Primzahl sein, so ist jede Zahl kleiner n nach Definition teilerfremd zu n.

Satz von Euler

Keine Sorge, das ist der letzte, aber auch wichtigste Teil der mathematischen Grundlagen, den wir uns ansehen müssen.
Der Satz von Euler besagt, dass für alle natürlichen Zahlen k, m und N mit $m<N$ gilt:

\[m^{k*\phi(N)+1} \mod N = m\]

Hier reicht es uns einfach, diesen Satz so hinzunehmen. Aber ein kleines Beispiel für die Vollständigkeit:

\(m=3, N=6, k=2\) Um $\phi(N)$ zu berechnen, können wir eine Primfaktorzerlegung anstellen, mit $p=2$ und $q=3$.
Dann gilt: \(\phi(N) = \phi(p*q) = (p-1)*(q-1) = 2\).
Zusammen:

\[3^{2*2+1} = 243\\ 243 \mod 6 = 3\]

Wenn wir uns überlegen, dass m unsere Nachricht ist, können wir über den Satz von Euler Ver- und Entschlüsseln.

RSA Algorithmus

Nachdem wir alle Grundlagen wiederholt haben, können wir uns den RSA Algorithmus ansehen.

Schlüsselgenerierung

Sehen wir uns zunächst an, wie die beiden Schlüssel generiert werden.

1. Wir wählen zunächst zwei sehr große Primzahlen p und q. Je größer die Primzahlen, desto schwieriger das Knacken der Verschlüsselung (in der Regel).
2. Nun berechnen wir $N = p*q$.
3. Als Nächstes berechnen wir $\phi(N)$. Dies wäre in der Regel sehr schwer und bei einem großen N nicht zu unserer Lebzeit berechenbar. Jedoch kennen wir beide Primfaktoren von N, deshalb gilt für uns \(\phi(N) = \phi(p*q) = \phi(p)*\phi(q) = (p-1)*(q-1)\). Das ist praktisch sehr leicht zu berechnen.
4. Wir wählen ein e mit \(1<e<\phi(N)\). Wichtig ist, dass $\text{ggT}(e, \phi(N)) = 1$, da wir für den privaten Schlüssel das multiplikative Inverse von $e\mod{\phi(N)}$ brauchen.
5. Wir berechnen dieses multiplikative Inverse d mit dem erweiterten Euklidischen Algorithmus: \(e*d \mod{\phi(N)}= 1\).
6. Der öffentliche Schlüssel besteht aus e und N. Also (e, N). Der private Schlüssel besteht aus (d, N).

Das Geheimnis des privaten Schlüssels, der unter allen Umständen geheim gehalten werden sollte, ist somit das multiplikative Inverse d. Um dies zu Berechnen, wird nämlich $\phi(N)$ benötigt. Wie bereits erwähnt, kann das nur in annehmbarer Zeit berechnet werden, wenn man die beiden Primfaktoren p, q kennt. Man kann deshalb auch behaupten, dass das eigentliche Geheimnis, die beiden Primfaktoren p und q sind.

Verschlüsselung

Wollen wir nun einen Text, verschlüsseln, müssen wir diesen zunächst in eine Zahl umwandeln. Dies können wir beispielsweise über die Unicode-Codierung tun. Diese Zahl m wird nun mit dem öffentlichen Schlüssel, bestehend aus e und N, verschlüsselt. Die Verschlüsselung funktioniert wie folgt:

\[c = m^e\mod{N}\]

Die daraus resultierende Zahl c, ist der Geheimtext, der unbesorgt übertragen werden kann.

Entschlüsselung

Wie bereits erwähnt wird der empfangene Text bzw. die Zahl mit Hilfe des privaten Schlüssels wieder entschlüsselt. Der private Schlüssel besteht aus dem multiplikativen Inversen d und dem Produkt N. Die Entschlüsselung funktioniert dabei so:

\[m = c^d\mod{N}\]

Der resultierende Text ist (hoffentlich) wieder unsere Nachricht in Unicode.

Das Warum?

Warum funktioniert das ganze? Sehen wir uns mal die Formel zur Entschlüsselung an: \(m = c^d\mod{N}\). Das c ist ja unser Geheimtext, und gleichzeitig auch aus dieser Formel entstanden: \(c = m^e\mod{N}\). Ersetzen wir nun c in der Formel für die Entschlüsselung, erhalten wir \(m = (m^e)^d\mod{N}\) (das erste Modulo können wir hier weglassen, da es hinten nochmal angewandt wird).
Wenden wir die Potenzgesetze an, erhalten wir \(m = m^{e*d}\mod{N}\). Wir wissen, dass d das multiplikative Inverse von $\phi(N)$ ist. Das bedeutet, dass \(e*d\mod{\phi(N)} = 1\) ist.

Jetzt wenden wir einen kleinen mathematischen Trick an. Wir können obigen Term umschreiben, in: \(e*d = k*\phi(N)+1\). Dabei ist k eine ganze Zahl. Wenn wir uns das kurz durch den Kopf gehen lassen, macht das durchaus Sinn. Da ein vielfaches, also k, von einer beliebigen Zahl, also $\phi(N)$, modulo dieser Zahl $\phi(N)$ immer 0 ergibt. Sprich die Division von \((k*\phi(N))\div \phi(N)\) ist immer restfrei.

Schreiben wir nun also wieder den Term um, in \(m = m^{k*\phi(N)+1}\mod{N}\). Und das sollte uns bekannt vorkommen, das ist nämlich der Satz von Euler. Deshalb, kommt beim Entschlüsseln eines verschlüsselten Textes wieder der Ursprungstext heraus.

Sicherheit

Wie bereits erwähnt beruht die Sicherheit der RSA Verschlüsselung auf der Schwierigkeit das multiplikative Inverse d zu berechnen ohne $\phi(N)$ zu kennen. Dieses ist nur einfach zu berechnen, wenn man die Primfaktoren p und q kennt, die N bilden. Die Berechnung von d wird auch oft als Trapdoor-Funktion, also Falltür-Funktion bezeichnet, da sie schwer zu berechnen ist, außer man kennt p und q.

Das $\phi(N)$ schwer zu berechnen ist, beruht auf der Annahme, dass es kein effizientes und schnelles Vorgehen gibt für die Zerlegung in Primfaktoren. Man sollte sich bewusst sein, dass dies eine Annahme ist, wo der Beweis noch nicht erbracht worden ist. Jedoch sollte man jetzt keine Albträume bekommen, dass seine Nachrichten oder Online-Banking Daten nicht mehr sicher wären, da sich schon viele schlaue Leute an der Primfaktorzerlegung die Zähne ausgebissen haben.

Es gibt jedoch eine andere, durchaus größere Gefahr. Mit der immer schnelleren Entwicklung von besseren Quantencomputern könnte die Primfaktorzerlegung tatsächlich in ein paar Jahrzehnten angegriffen werden. Wie das ganze funktioniert, werde ich im nächsten Artikel beleuchten.
Warum sollte man sich dafür interessieren, dass RSA in 20-30 Jahren nicht mehr sicher ist? Es existiert eine Überwachungsstrategie mit dem Namen: Harvest now, decrypt later, was soviel heißt wie Sammel jetzt, entschlüssele später. Angreifer sowie Geheimdienste sammeln jetzt schon Daten, mit der Hoffnung diese in Zukunft entschlüsseln zu können. Deshalb geht der Trend hin zu Verschlüsselungsmethoden, die nicht auf der Primfaktorzerlegung beruhen und Quanten Sicher sind.

Credit

Vieles aus den mathematischen Grundlagen habe ich von Florian Dalwik. Schaut mal gerne bei seinem Kanal vorbei und vor allem bei dem hervorragenden RSA Video.

Danke fürs Lesen, bleibt neugierig