Im ersten Teil meiner Serie: “Die Schönheit der Algorithmen und Datenstrukturen” will ich eine kleine Einführung in die Graph-Algorithmen geben. Dies will ich Anhand eines Beispieles versuchen. Wie funktioniert eigentlich so ein Navi?

Achtung: Wie in den anderen Teilen der Serie werde ich auch hier in einigen Teilen stark vereinfachen. Dieser Text soll vor allem neugierig machen und nicht terminologisch 100% korrekt sein.

Lass mal annehmen, wir sind in eine neue Stadt gezogen und wollen nun zu einer Adresse nur paar Häuser weiter. Weil wir uns noch nicht auskennen, nehmen wird das Navi zur Hand.

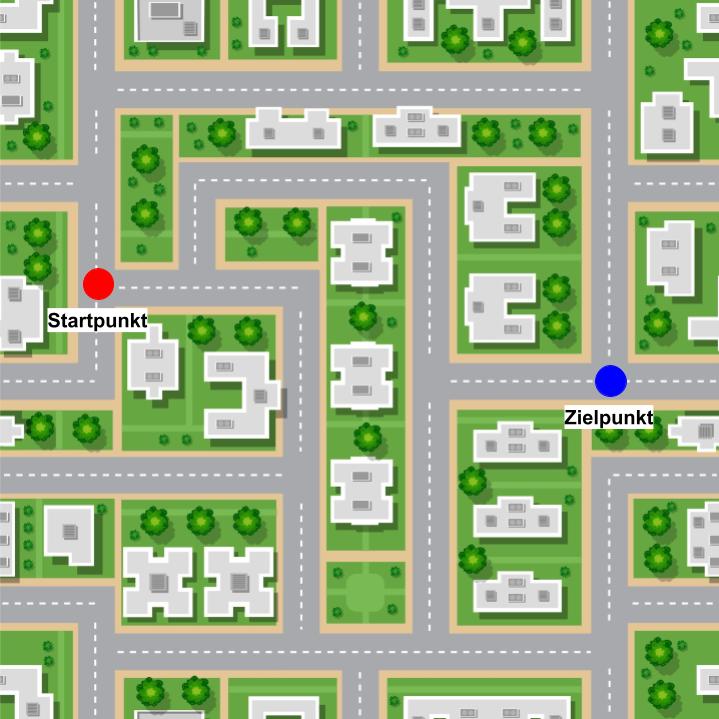
Die Informationen, die wir unserem Navi anvertrauen, sind “Wo sind wir gerade?” (Startpunkt) und “Wo wollen wir hin?” (Zielpunkt).

Woher weis unser Navi nun, welchen Weg wir nehmen müssen, um am schnellsten zu unserem Ziel zu gelangen?

Um diese Frage zu beantworten zu können müssen wir uns zunächst ansehen, wie das Handy die Daten des Navis abspeichert.

Graphentheorie

Eine Möglichkeit die Wege der Stadt abzuspeichern bietet die Graphentheorie. Hauptbestandteil dieser Theorie sind die namensgebenden Graphen. Ein solcher Graph besteht aus einer Menge von Knoten und Kanten. Ein Beispiel für einen Graphen ist im nächsten Bild zu sehen. Dieser Graph hat sechs Knoten und sieben Kanten.

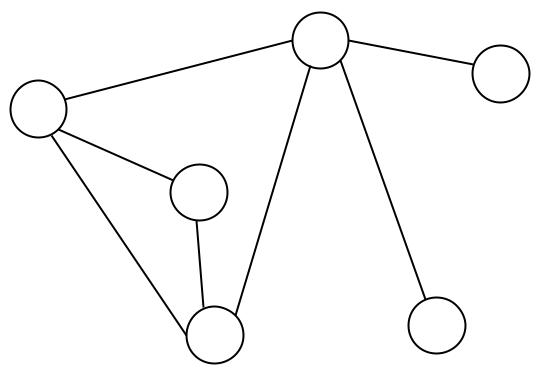
Graphen kann man als Modelle für viele Strukturen, wie sie in der Natur vorkommen, benutzen.

Zum Beispiel kann ein Telefonnetz als Graph abgebildet werden, hierbei sind die einzelnen Telefone die Knoten und die Leitungen der Telefone die Kanten des Graphen. Aber auch ein Soziales Netzwerk, also wer kennt wen, kann über einen Graphen abgebildet werden. Die Knoten wären in diesem Fall die Personen und deren Beziehung die Kanten. Zwei Knoten würden in dem Fall nur durch eine Kante verbunden werden, wenn sich die beiden Personen kennen.
In der Graphentheorie gibt es des Weiteren eine Menge an Algorithmen (also Lösungswege) womit man Probleme in einem Graphen lösen kann. So einen Algorithmus werden wir später für unsere Navi-App einsetzen.

Stadtplan als Graph

Wie können wir nun aus dem Stadtplan einen Graph erzeugen, der uns mit unserem Problem weiterhelfen kann?
Eine Lösung kann sein, dass wir einen Graph erstellen, bei dem die Straßen der Stadt die Kanten sind und die Kreuzungen die Knoten. Ich habe das mal im folgendem Bild versucht darzustellen.

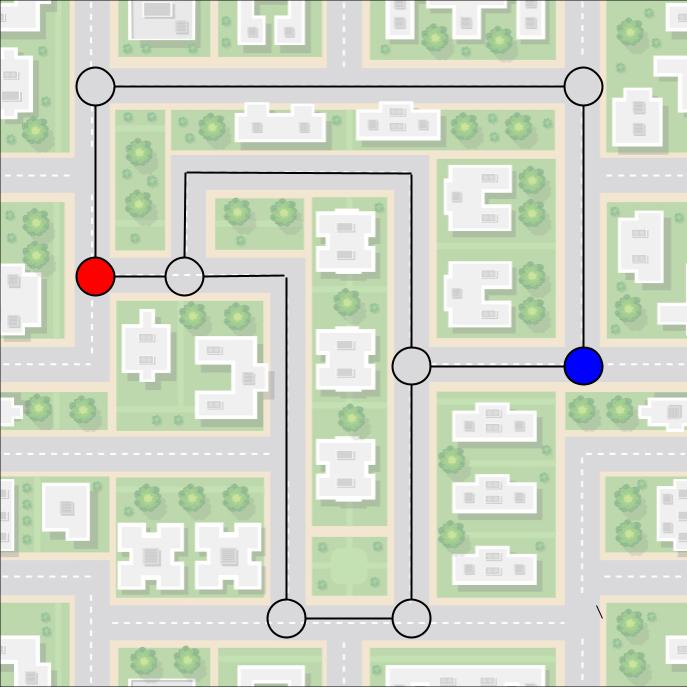
Nun ist es bei Graphen in der Graphentheorie so, dass die Länge und Lage von Knoten und Kanten keine Rolle spielen. Dies ist auch in diesem Bild zu sehen. Die zwei Graphen links und rechts, sind in der Graphentheorie völlig identisch.

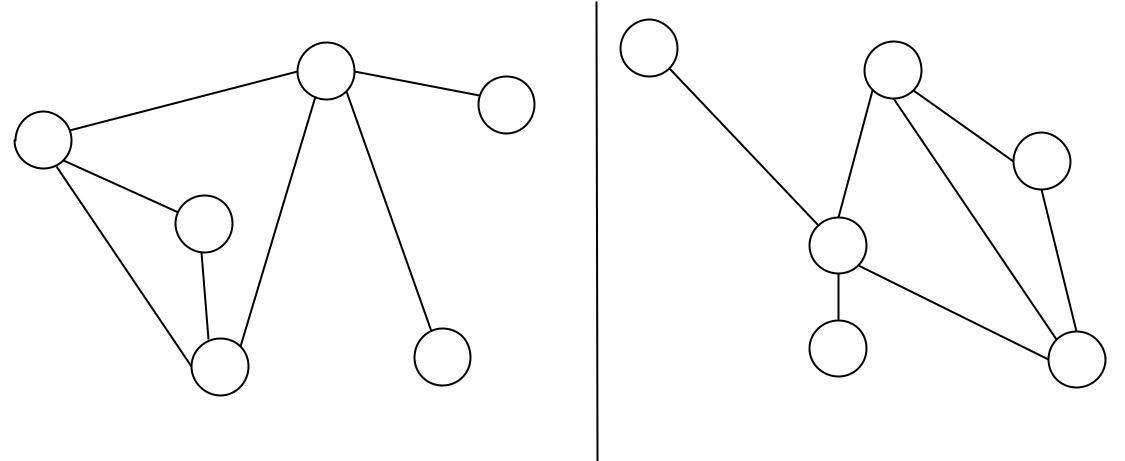
Dies ist jedoch ein Problem für uns, da für den Graph eine kurze und eine sehr lange Straße völlig identisch ist.
Wir brauchen also eine Möglichkeit den einzelnen Kanten eine Zahl zuzuordnen. Dies kann zum Beispiel die Zeit sein, die wir benötigen um vom Anfang bis zum Ende der Straße zu gelangen. Diese Werte werden Gewichte der Kanten genannt. Das nächste Bild ist fas identisch zum vorherigen, nur das nun die Gewichte (oder auch Minuten) an den Kanten stehen.

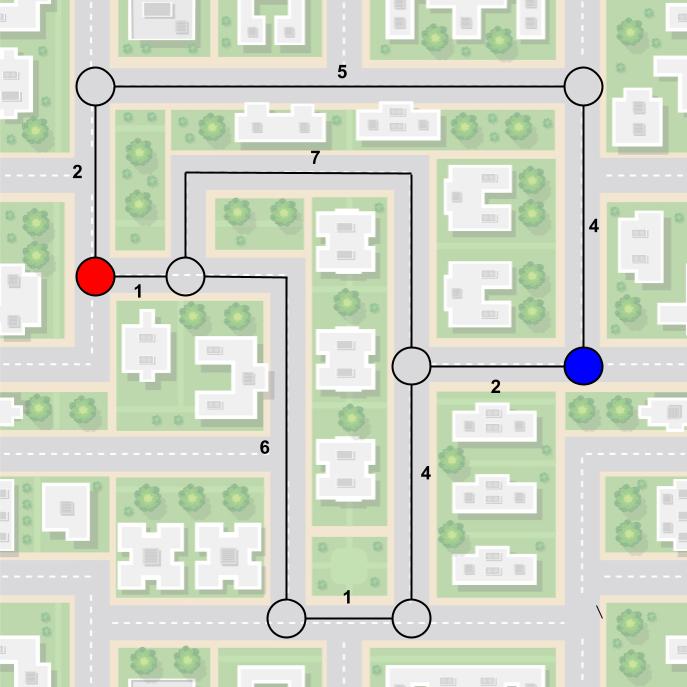
Algorithmus von Dijkstra

Was können wir jetzt mit unserem gerade erstellten Graphen tun? Eigentlich eine ganze Menge. Die Frage ist jedoch was wollen wir tun? Wir wollen einen Weg zwischen Start- und Endpunkt über die Kanten finden. Dabei soll der Weg so schnell wie möglich sein, also die Anzahl der Minuten (Gewichte) so gering wie möglich sein. Dieses Problem wird auch Single-source shortest path bezeichnet.

Ein sehr bekanntes Verfahren ist der Dijkstra-Algorithmus. Das Verfahren wird uns dabei helfen, einen kürzesten Pfad zu finden.

Wie funktioniert der Dijkstra-Algorithmus? Ich versuche die Frage so einfach wie mir möglich zu beantworten.

1. Jeder Knoten bekommt einen zusätzlichen Wert. Dieser sagt aus, in wie vielen Minuten er vom Startpunkt aus erreichbar ist. Zunächst bekommen alle Knoten den Wert Unendlich. Bis auf den, der den Startpunkt darstellt. Dieser bekommt den Wert 0, denn da er ja den Start darstellt, benötigen wir keine Zeit um von ihm zu ihm zu gelangen. Dieser gilt außerdem bereits als besucht.
2. Nun werden alle Knoten untersucht, die noch nicht besucht wurden und mit den bereits besuchten Knoten verbunden sind. Der Knoten, der am schnellsten (aufsummierte Minuten) vom Startknoten aus erreichbar ist wird als nächstes besucht.
3. Berechne für alle noch unbesuchten Nachbarknoten die Gesamt-Minuten. Wenn dieser Wert kleiner als die dort gespeicherte Minutenanzahl ist, aktualisiere diesen Wert.
4. Solange noch nicht alle Knoten besucht worden sind, gehe zu Schritt 2.
   
   Ich weiß, dass diese Erklärung etwas kompliziert wirkt. Deshalb habe ich versucht, dass in einer Animation darzustellen.

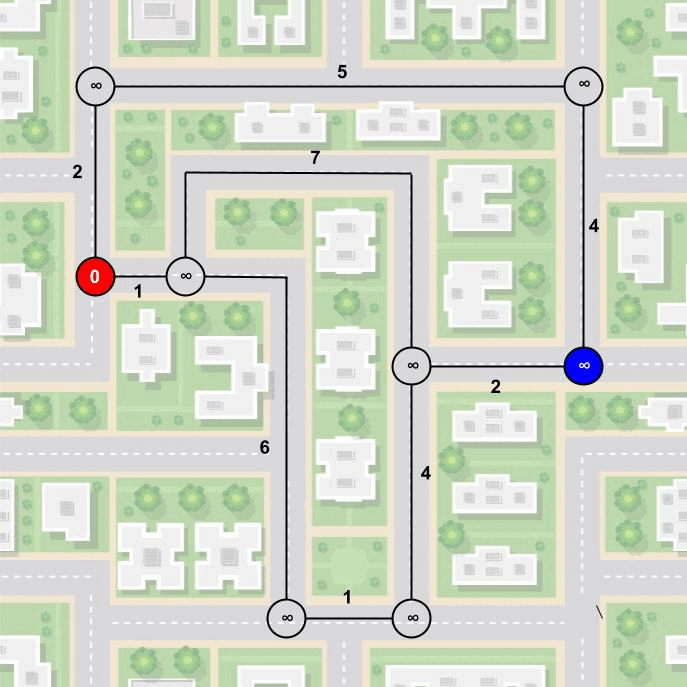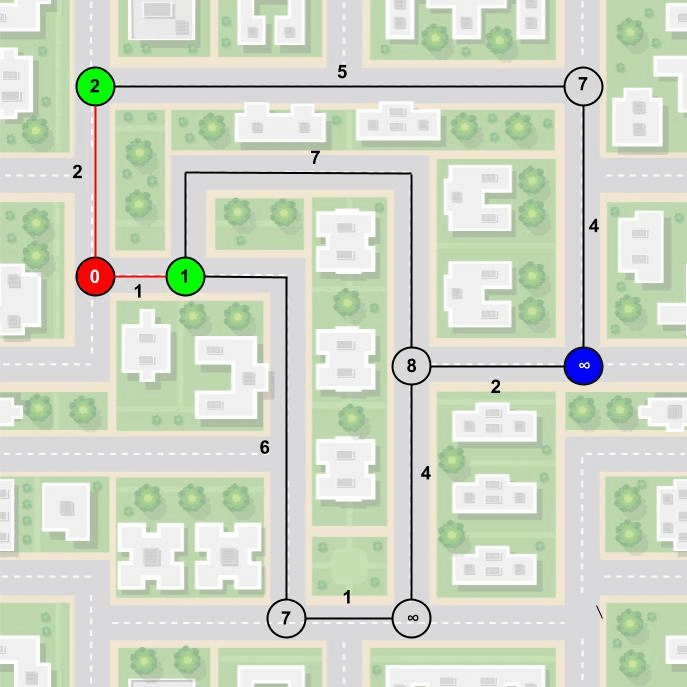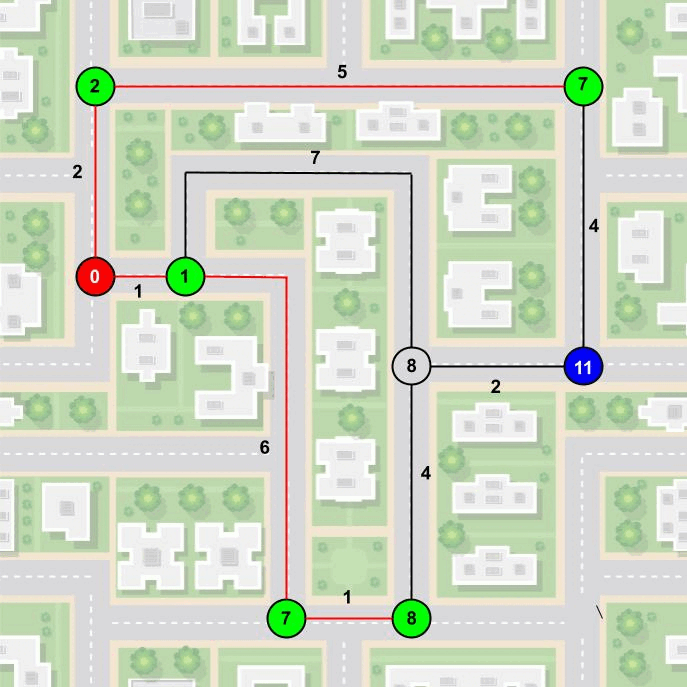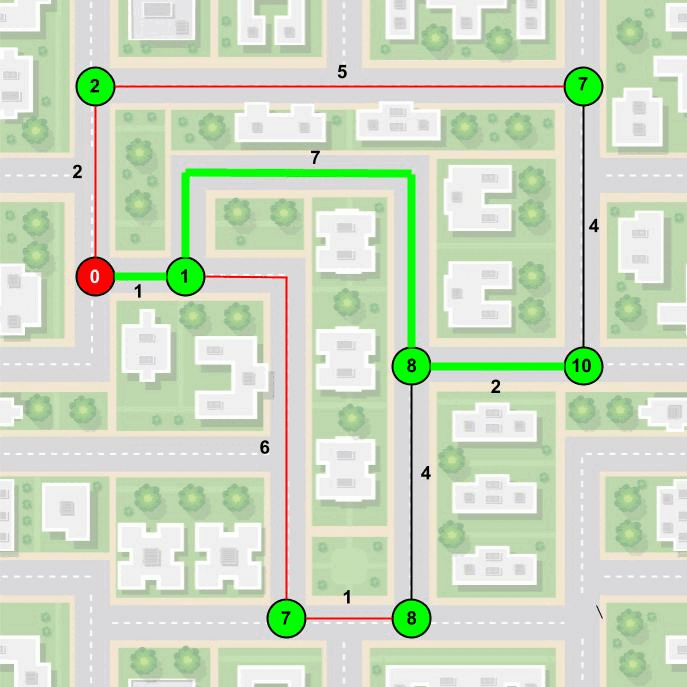
So kann der Algorithmus von Dijkstra den kürzesten Weg finden. Eine Weitere spannende Frage ist, warum ist das immer der kürzeste Weg? Oder, funktioniert der Algorithmus von Dijkstra auch mit negativen Werten? Beide Fragen kann man sich mal an einem verregneten Samstagnachmittag selbst stellen und beantworten :)

Abschließend bleibt noch zu sagen, dass es noch andere tolle Algorithmen gibt, um in solch einem Graph-Netzwerk den kürzesten Weg zu finden. Jedoch ist, wie ich finde, der Algorithmus von Dijkstra ein guter Einstieg in diese Welt.

Danke fürs lesen, bleibt neugierig.