Im Lockdown habe ich mich (wie viele andere auch) von Dominos ernährt. Nicht weil Dominos besonders gut oder günstig ist, aber sie sind einfach sehr schnell bei der Lieferung. Das ganze gipfelte sogar darin, dass mein Bruder mir einen Dominos Gutschein zu Weihnachten besorgt hat :)

Da ich viel Zeit in der Dominos App verbracht habe, ist mir irgendwann aufgefallen, dass man einige Pizzen billiger bekommt, wenn man etwas mit den Zutaten rumspielt. Die Frage, die sich dann aufdrängte, ist: Welche Pizzen kann ich billiger bekommen und wie muss ich dafür mit den Zutaten hantieren.

Ein kurzer Hinweis: Mit dieser Technik lässt sich nicht viel Geld sparen. Es geht meist nur um ein paar Cent bis hin zu 2 €. Aber man kann die Graphentheorie nutzen, das macht es cool. Noch etwas: Wenn ihr Pizzen wollt, bestellt sie bei lokalen Pizzarien. Auch wenn diese nicht liefern, ist es es wert die Pizzen abzuholen.

Was ist los bei Dominos?

Lasst mich zunächst mal erklären, wieso man bei den Preisen von Dominos überhaupt rumspielen kann. Bei Dominos gibt es ca. 30 Pizzen und ca. 40 verschiedene Zutaten. Die Zahlen können variieren, da es immer wieder Saisons Angebote gibt. Jedoch gibt es einen festen “Pizzen-Stamm” auf den ich mich hier beziehen werde.
Jede Pizza besteht aus einer Auswahl aus den 40 Zutaten. Zum Beispiel befindet sich auf der Pizza Funghi Champignons, Käse und Basilikum-Pesto.
Um allen Kundenwünschen gerecht zu werden, kann man nun beliebige zusätzliche Zutaten auf die Pizza drauflegen bzw. herunternehmen. Man könnte also die Champignons der Pizza Funghi entfernen und Ananas dafür hinzufügen.

Wie sieht es jetzt mit dem Preis unserer selbst entweihten Pizza Funghi aus? Die Champignons haben einen Preis von 1,39 € und die Ananas kostet 2,09 €. Die Pizza Funghi kostet 11,49 €. Führen wir jetzt unsere Änderungen durch, wird der Preis der Champignons abgezogen und der für die Ananas dazu addiert. Die neue Pizza kostet also 12,19 €.

Es gibt noch zwei Regeln, die Dominos (wahrscheinlich aus Gründen der Gewinnoptimierung) durchsetzt. Erstens, entfernt man mehrere Zutaten, so darf man nur den Preis der teuersten Zutat abziehen. Zweitens, eine Pizza kann durch Änderungen nur teuerer werden, aber nie billiger als ihr Ursprungspreis.

Ka-Ching!

Wie können wir diese Regeln ausnutzen?
Wir wollen jetzt eine Pizza Salami bestellen. Diese kostet 11,99 € und besteht aus Käse und Salami. Wir machen jetzt einen kleinen Umweg über die Pizza Caprese. Die Pizza Caprese kostst nur 11,49 € und besteht aus Käse, Mozzarella, Basilikum-Pesto und Tomaten. Um aus der Pizza Caprese eine Pizza Salami zu machen, müssen Mozzarella, Pesto und Tomaten runter und die Salami hinauf. Wie sieht jetzt der Preis aus?
Die teuerste zu entfernende Zutat ist der Mozzarella mit 2,29 €. Die Salami, die wir hinzufügen, kostet 2,09 €. Wenn wir nun wie üblich den Preis berechnen, würde unsere modifizierte Pizza Caprese 11,29 € kosten. Wie oben in den Regeln bereits erwähnt, hält sich Dominos hier vor, von dem ursprünglichen Preis der Pizza Caprese nicht abzuweichen.
Wir haben also jetzt eine Pizza Salami erstellt, die statt 11,99 € nur 11,49 € kostet. Ka-Ching!

Natürlich habe ich das ganze auch ausprobiert. Hier seht ihr zwei Pizzen frisch von Dominos bestellt. Eine für 11,99 € und die andere für 11,49 €. Da ich selber nicht erkennen konnte, welche der beiden die “echte” Salami Pizza war, sehe ich den Test als bestanden an.

Welche Pizzen muss man in Zukunft bestellen?

Das geht leider nicht mit jeder Pizza. Die Aufgabe ist es nun rauszufinden, bei welcher Pizza eine Vergünstigung möglich ist. Und was fast noch wichtiger ist, wie der Weg der Vergünstigung aussieht.
Natürlich könnte man das stumpf durchrechnen, aber das würde Stunden dauern. Lieber schreibe ich wochenlang an einem Programm, dass das ganze auf eine “Informatiker-Weise” löst.

Die Idee zur Lösung kam mir recht spontan und ich weiß nicht, ob es noch bessere Lösungen gibt. Um das ganze Nachvollziehen zu können, ist es wichtig, die Grundlagen der Graphentheorie zu kennen. Ich habe dazu auch schon einen Artikel verfasst.

Wir versuchen nun die gesamte Preisgestaltung in einem Graphen darzustellen. Die Pizzen sind unsere Knoten und die Preise sind unsere Kanten.

Ich habe in diesem Graph nur 3 Pizzen dargestellt, da es sonst schnell unübersichtlich wird. Man kann hier zum Beispiel sehen, dass man von der Pizza Caprese ohne Aufpreis auf die Pizza Salami kommt. Ist nichts Neues, haben wir ja schon festgestellt. Eine wichtige Information ist nun jedoch in diesem Graph verloren gegangen. Der Basispreis jeder Pizza. Diese Info ist sehr wichtig, da wir jetzt nicht wissen, ob es Billiger ist, die Pizza Salami direkt zu bestellen oder über den Umweg der Pizza Caprese zu gehen.

Um das zu lösen, kann ein Hilfsknoten hinzugefügt worden. Ich nenne ihn mal Start (warum wird evtl. später klar). Dieser wird mit jeder Pizza verbunden. Die Kanten bekommen den Basispreis der jeweiligen Pizza als Gewicht.

Jetzt haben wir alle Informationen, die wir benötigen. Wir können uns nun zum Beispiel alle Preise für die Pizza Salami ansehen. Dafür gehen wir vom Startknoten über jeden möglichen Weg zur Pizza Salami und summieren dabei die Preise auf. In unserem Beispiel bekommen wir jetzt drei Preise: 11,99 €, 11,49 € und 12,19 €. Was jetzt natürlich sinnvoll ist, wenn wir uns nur die Wege mit dem günstigsten Preis ausgeben/ansehen.

Wenn das nicht nach Dijkstra schreit, weiß ich auch nicht. In dem oben verlinkten Kapitel habe ich bereits erklärt, wie der Dijkstra-Algorithmus funktioniert, deshalb erspare ich mich hier die Erklärung. Jetzt sollte auch klar werden, warum ich hier einen Graphen zur Darstellung gewählt habe und warum ich den ersten Knoten “Start”-Knoten genannt habe. Führen wir nun nämlich Dijkstra vom Startknoten zu jedem anderen Knoten aus, bekommen wir für jede Pizza die günstigste Konfiguration und den besten Preis geliefert.

Wie man die Kantengewichte berechnet

Noch ein paar kurze Sätze zu den Preisen an den Katen. Wie werden diese berechnet. Es gehören immer zwei Knoten (Pizzen) zu einer Kante. Die “Ausgangs”-Pizza und die “Ziel”-Pizza. Nun nimmt man die Ausgangspizza und entfernt alle Zutaten, die sich nicht auf der Zielpizza befinden und fügt im Anschluss die Zutaten, die fehlen hinzu. Natürlich dürfen wir die Regel, die für mehrere hinzugefügte Zutaten gilt, nicht vergessen und auch nicht, dass die Ausgangspizza nicht billiger werden kann. Im Übrigen: Das die Ausgangspizza nicht billiger werden kann, spielt uns gut in die Karten. Wir haben nämlich so keine negativen Kantengewichte. Das ist die Voraussetzung um Dijkstra anwenden zu können.

Will code for food

Ich habe das ganze jetzt mal in C++ implementiert. Den Code findet ihr auf GitHub. Alle Pizzen mit sämtlichen Zutaten sind in einer SQLite Datenbank hinterlegt, die auch dort zu finden ist. Natürlich will ich euch die Ausgabe meines Programmes nicht vorenthalten.

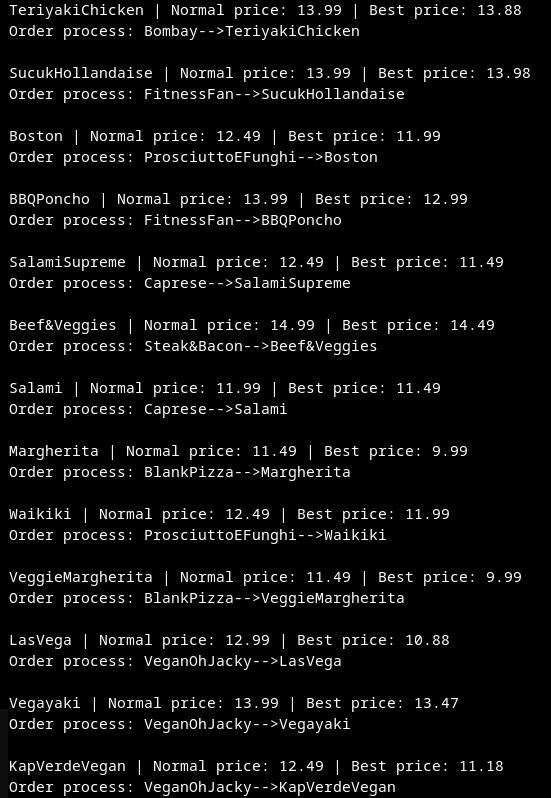
Alle Pizzen, die billiger bestellt werden können, sind hier mit ihren Preisen aufgelistet. Darunter befindet sich der beste Weg, diese Pizzen zu bestellen.

Zum Schluss: Es gibt zu dem Thema auch einen Talk. Dort wird die Berechnung jedoch nicht mit einem Graphen gelöst, sondern über einen Brute-Force Ansatz.

Mehr wollte ich schon gar nicht loswerden :)

Danke fürs Lesen, bleibt neugierig