Im letzten Teil meiner Serie: “Die Schönheit der Algorithmen und Datenstrukturen” möchte ich auf eines der größten ungelösten Probleme der Informatik eingehen.
Gleich eine Warnung zuvor, dieser Artikel wird lange. Aber es lohnt sich, die Problemstellung ist wirklich verständlich und es winkt ein großes Preisgeld für die Lösung (neben dem Ruhm und der Ehre).

Achtung: Wie in den anderen Teilen der Serie werde ich auch hier in einigen Teilen stark vereinfachen. Dieser Text soll vor allem neugierig machen und nicht terminologisch 100% korrekt sein.

Ich werde hier auch auf Konzepte eingehen, die ich in den vorangegangenen Artikeln erläutert habe. Also: Be prepared!

Überblick

Erstmal ein kurzer Überblick um uns etwas zu sortieren. Über was reden wir hier eigentlich. P und NP sind zwei Klassen von Problemen. In P liegen alle Probleme die “schnell” lösbar sind. Hingegen liegen in NP alle Probleme deren Lösung “schnell” überprüfbar sind. Etwas allgemeiner ausgedrückt liegen alle Probleme die “schnell” lösbar sind in P und die Probleme die “sehr schwer” lösbar sind (meist) in NP. Die Millionenfrage ist nun, sind die beiden Klassen identisch? Das heißt ist ein Problem welches in NP liegt gleichzeitig in P? Gibt es also eine Möglichkeit sehr schwere Probleme trotzdem leicht und schnell zu lösen. Wer diese Frage beantworten kann (egal ob mit ja oder nein) ist eine Million US-Dollar reicher, jedoch hat das bis jetzt niemand geschafft.
Übrigens, viele der Verschlüsselungsverfahren basieren auf der Hoffnung, dass $P \neq NP$ ist. Sollte also das Gegenteil bewiesen werden, müssen wir auf solche Sachen wie z.B. Online-Banking verzichten.

Begriffserklärung

Was bedeutet jetzt dieses P und NP. Lasst euch nicht von den Fachbegriffen abschrecken, ich versuche die im Laufe des Artikels zu erklären.

P

P steht für Probleme die in polynomieller Laufzeit lösbar sind. Also alle Probleme die in ihrer O-Notation “nur” ein Polynom besitzen. Also sind Probleme, deren Lösungen mit Verfahren mit Laufzeiten von $\mathcal{O}(1)$, $\mathcal{O}(n)$, $\mathcal{O}(n^2)$, $\mathcal{O}(n^3)$, usw. gefunden werden können, alle in P. Wenn wir uns an die vorangegangenen Probleme die wir besprochen haben erinnern, haben wir bis jetzt nur solche kennengelernt, die eindeutig in P liegen. Probleme, die beispielsweise nur mit Algorithmen gelöst werden können, die eine Laufzeit von $\mathcal{O}(2^n)$ haben, liegen nicht in P.

NP

NP steht für alle Probleme, die in nichtdeterministischer polynomieller Laufzeit lösbar sind. Der Unterschied ist also nur der Zusatz nichtdeterministisch. Im Großen und Ganzen müssen NP Probleme Lösungen besitzen, die in polynomieller Laufzeit überprüfbar sind. Wie wir zu dieser Lösung kommen ist hier nicht wichtig.

Sudoku

Was hat das ganze jetzt mit “nichtdeterministisch” zu tun? Das würde ich gerne an einem Beispiel zeigen. Dafür nehme ich das Spiel Sudoku (falls ihr mit den Regeln nicht vertraut seit, ist es hilfreich diese schnell nachzulesen).
Für das Beispiel würde ich gerne das Spiel etwas abändern. Wir spielen nicht auf einem 9x9-Feld, sondern auf einem nxn-Feld (n steht hier wieder für eine beliebig große Zahl). Des Weiteren ist bei uns am Anfang kein einziges Feld ausgefüllt. Das Ziel ist es nun, eine gültige Lösung für das nxn-Feld zu finden.

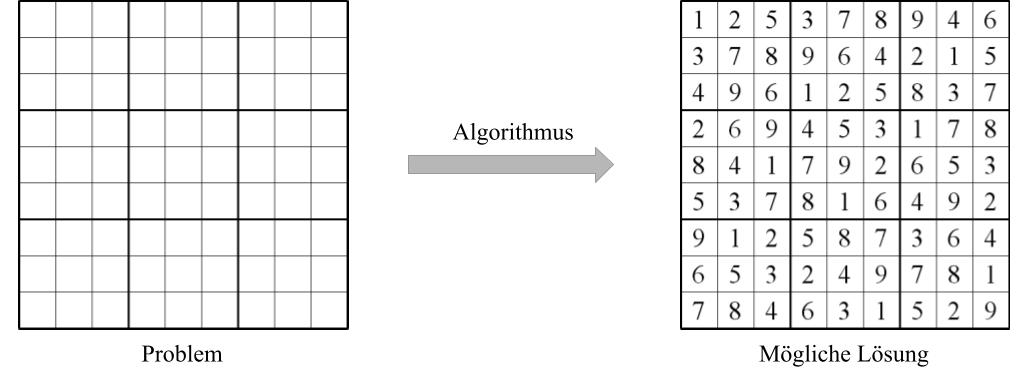
Konstruktion eines Algorithmus

Unser hypothetischer Algorithmus könnte nun einfach eine Lösung raten und diese danach überprüfen. Ist die Lösung regelkonform ist er fertig, wenn nicht rate und überprüfe eine neue. Das ganze geht so weiter, bis der Algorithmus eine regelkonforme Lösung für unser Spielfeld ausgibt.

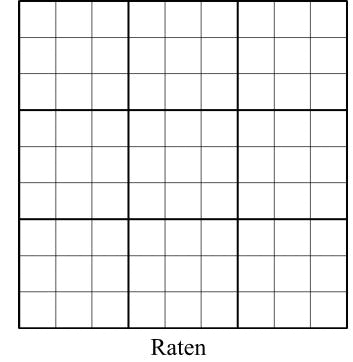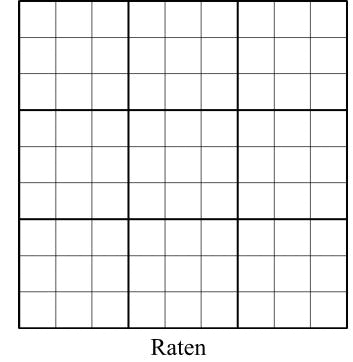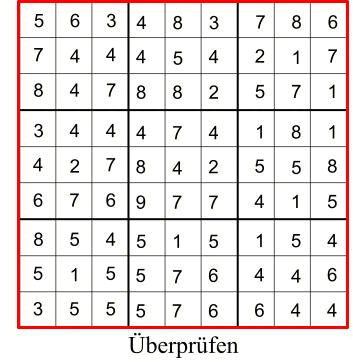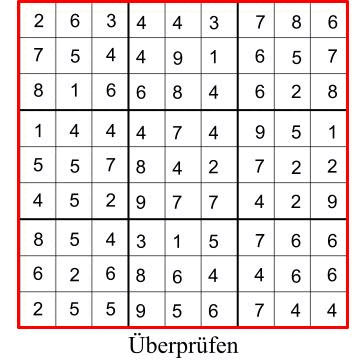
Was ist nun hier die Laufzeit? Nun wir müssen raten und überprüfen. Das Raten ist einfach, wir haben $n^2$ viele Felder und füllen jeweils eine willkürliche Zahl dort hinein. Für das Raten haben wir also eine Laufzeit von $\mathcal{O}(n^2)$. Das Überprüfen ist auch trivial, wir müssen nur jede Spalte, jedes Zeile und jedes Kästchen überprüfen. Wir haben n Spalten, n Zeilen und n Kästchen. Also hat das überprüfen eine Laufzeit von $\mathcal{O}(3n)$. Der Knackpunkt ist nun, wie oft müssen wir raten, bis wir eine regelkonforme Lösung gefunden haben? Im schlimmsten Fall müssen wir alle möglichen Belegungen des Spielfeldes durchgehen. Ich hoffe meine Statistik Kenntnisse verlassen mich da jetzt nicht, aber das müssten $2^{n^2}$ Möglichkeiten sein. Also hat unser hypothetische Algorithmus eine Worst-Case Laufzeit von $\mathcal{O}(2^{n^2})$. Das ist sicher nicht mehr polynomiell. Aber ist es nichtdeterministisch polynomiell?

Die Sache mit dem Nichtdeterminismus

Nichtdeterminismus ist ein theoretisches Konzept in der Informatik. Am Beispiel unseres hypothetischen Algorithmus heißt es, dass er sich gleichzeitig alle möglichen Spielfeld Besetzungen ansieht und eine regelkonforme auswählt. Und das tut er, ohne sich jede einzelne anzusehen. Wie können wir so einen Algorithmus bauen? Ganz einfach, wir nehmen eine Kristallkugel und bauen diese in unseren Computer mit ein. Die Kristallkugel sagt uns dann für jedes einzelne Feld, welche Zahl reinkommen muss um eine regelkonforme Lösung zu enthalten.

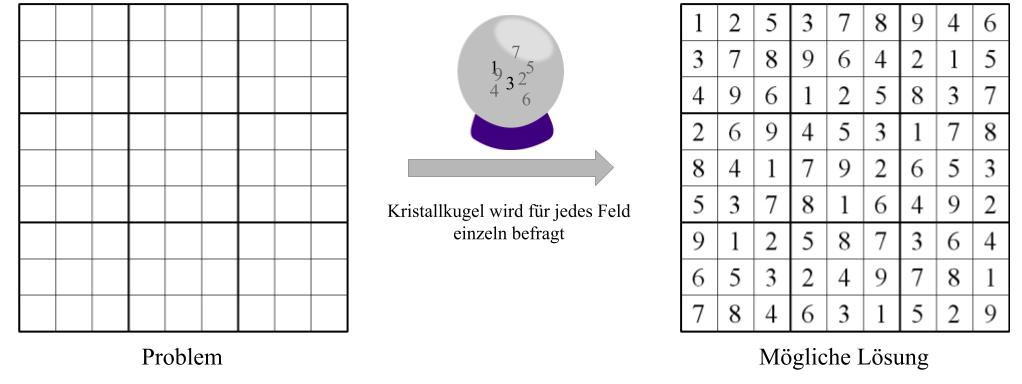
Da es $n^2$ viele Felder gibt, hat unser Algorithmus nun eine Laufzeit von $\mathcal{O}(n^2)$. Die Kristallkugel kennt den Weg zur Lösung und verrät sie unserem Algorithmus. Genau das ist der Nichtdeterminismus.

Wenn also ein Computer mit einer solchen Kristallkugel das Problem in polynomieller Laufzeit lösen könnte, dann liegt unser Problem in NP.

P vs. NP

Um ein Problem P bzw. NP zuschreiben zu können, muss das Lösungsverfahren polynomielle Laufzeit bzw. nichtdeterministisch polynomielle Laufzeit haben. Wir haben ja zuvor definiert, dass ein NP-Problem eine Lösung besitzen muss, die in polynomieller Laufzeit überprüfbar sein müssen.
Wenn man darüber nachdenkt, dann wird klar, dass jedes P-Problem auch ein NP-Problem ist. Denn man kann ja jede Lösung eines P-Problems überprüfen, indem man diese einfach nochmal ausrechnet und vergleicht.
Das können wir uns am Beispiel des Sortierens nochmal ansehen. Wir haben gesehen, dass es Verfahren gibt, die einen Kartenstapel mit Laufzeit $\mathcal{O}(n\log{n})$ sortieren können. Das macht es eindeutig zu einem P-Problem. Aber wir können die Lösung, also den sortierten Kartenstapel überprüfen (also schauen ob er wirklich sortiert ist), indem wir das Verfahren einfach noch einmal auf den sortierten Kartenstapel anwenden. Wenn sich nichts ändert, ist die Lösung valide. Also können wir die Lösung auch mit Laufzeit $\mathcal{O}(n\log{n})$ überprüfen. Das macht das ganze zu einem NP-Problem.
Also zu welcher Klasse gehört das Problem des Sortierens nun? Die Frage ist schnell beantwortet, denn jedes P-Problem ist auch ein NP-Problem.

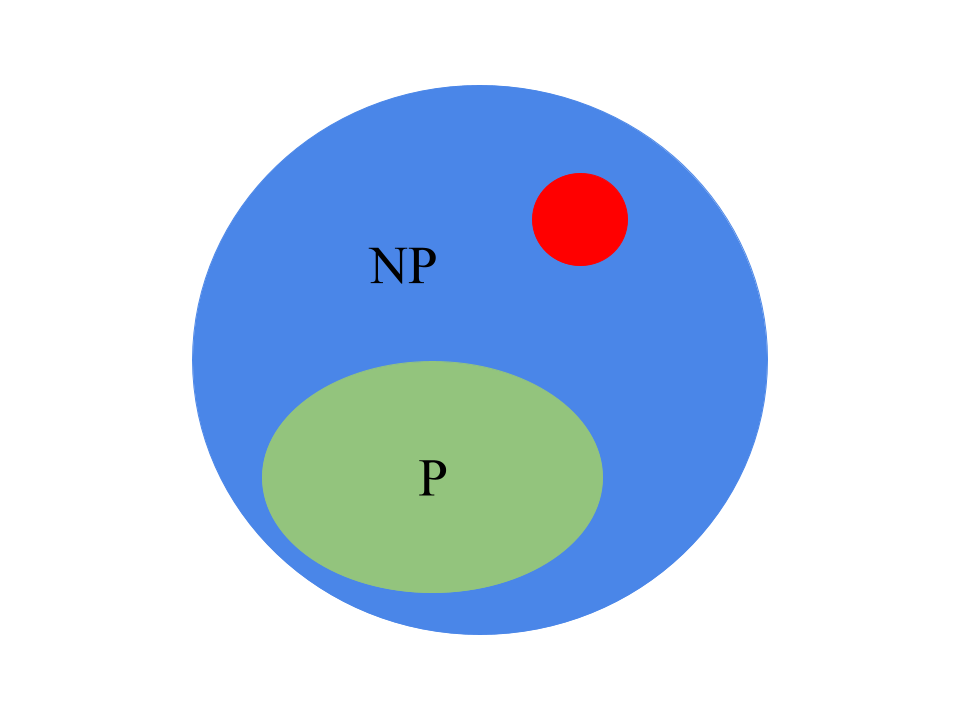
In der Grafik wird klar wie die aktuelle Sicht auf die Klassen aussieht. Die P-Probleme liegen in der Menge NP. Aber kein NP-Problem liegt in P (ob das wirklich so ist bleibt immer noch ein Rätsel). Welche Rolle der rote Kreis spielt, wird im nächsten Abschnitt beantwortet.

Die NP-Klasse

Alle Probleme in der Informatik (wie zum Beispiel das Sortieren oder Navigieren) lassen sich wie gesagt in P bzw. NP klassifizieren. Oft hat man festgestellt, dass ein Problem, von dem man angenommen hat, dass es in NP liegt (und schwer lösbar war), doch in P liegt. Man hat einfach einen Verfahren gefunden das Problem schnell und effizient zu lösen. Um die Frage am Anfang des Artikels nochmal aufzugreifen: Ist das für alle Probleme möglich die man zurzeit NP zuschreibt?
Die Antwort ist wortwörtlich eine Million Dollar wert.

Für einige sehr bekannte Probleme wurde bisher noch kein schnelles Verfahren gefunden. Jedoch hat man festgestellt, dass diese Probleme sich den selben “Kern” teilen. Das bedeutet, dass wenn ein schnelles Verfahren für eines dieser Probleme gefunden wird, alle Probleme durch dieses schnelle Verfahren gelöst werden können.
Die Klasse dieser Probleme mit dem selben “Kern” heißt “NP-Vollständig”. Diese Klasse wird durch den roten Punkt repräsentiert.
Wird ein schnelles Verfahren (also ein Verfahren mit polynomieller Laufzeit) für ein NP-Vollständiges Problem gefunden gilt sofort $P = NP$. Das wäre schon der Beweis den einem das große Geld und den großen Ruhm einbringt.

NP-Vollständig

Im folgenden Kapitel möchte ich zwei der NP-Vollständigen Probleme vorstellen.

Dreifarbenproblem

Für dieses Problem benötigen wir etwas Vorwissen aus den vorangegangenen Kapiteln. Genauer gesagt müssen wir wissen was ein Graph ist.
Wir haben nun einen beliebigen Graphen vor uns und drei verschiedene Farben (z.B. rot, blau und grün). Das Dreifarbenproblem ist nun zu Entscheiden, ob der Graph so färbbar ist, sodass jeder Knoten eine andere Farbe hat als sein Nachbarknoten. Ich versuche das mal in einem Bild klarzustellen. Links ist ein Graph zu sehen, der nicht nach diesen Regeln einfärbbar ist. Egal wie lange man das versucht, man wird keine gültige Belegung finden. Rechts hingegen ist ein Graph abgebildet, der nach den Regeln des Dreifarbenproblem einfärbbar ist. Ich habe mir erlaubt ihn schon mit einer beispielhaften Färbung zu zeigen.

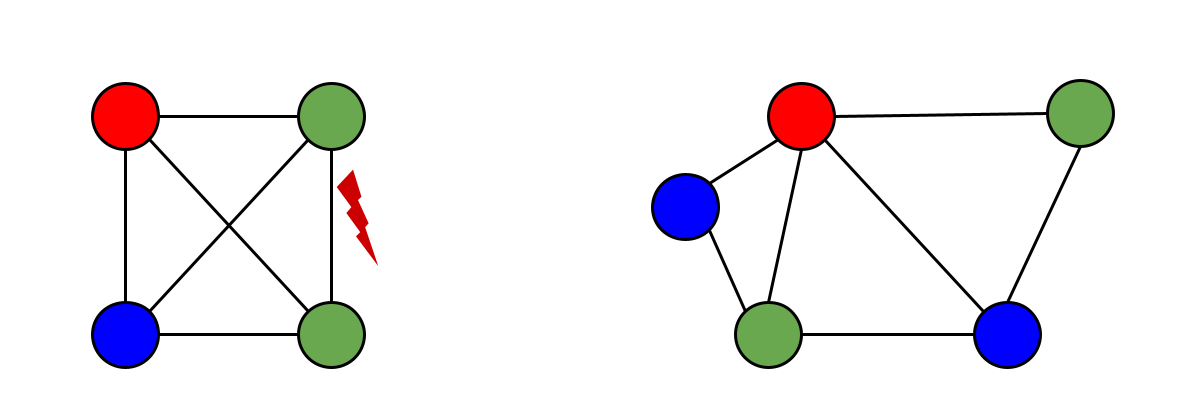
Die Ausgabe für das Dreifarbenproblem ist also beim linken Graph NEIN und beim rechten Graph JA. Wenn wir also ein Verfahren finden was die Frage schnell beantworten kann, hätten wir P vs. NP gelöst.

Das Problem des Handlungsreisenden

Auch für dieses Problem müssen wir wissen was ein Graph ist.
Stellen wir uns mal folgendes Szenario vor. Ein Lieferando-Fahrer ist gerade bei einem sehr beliebten Restaurant. Fünf Kunden haben in diesem Restaurant etwas über die Lieferando-App bestellt. Der Fahrer muss nun also von dem Restaurant zu den fünf Kunden fahren. Da das Restaurant so beliebt ist, muss er nach dieser Fahrt wieder zu diesem Restaurant zurück.
Das Problem des Handlungsreisenden ist es nun, die kürzeste Route zu finden, die der Lieferando-Fahrer nehmen sollte.

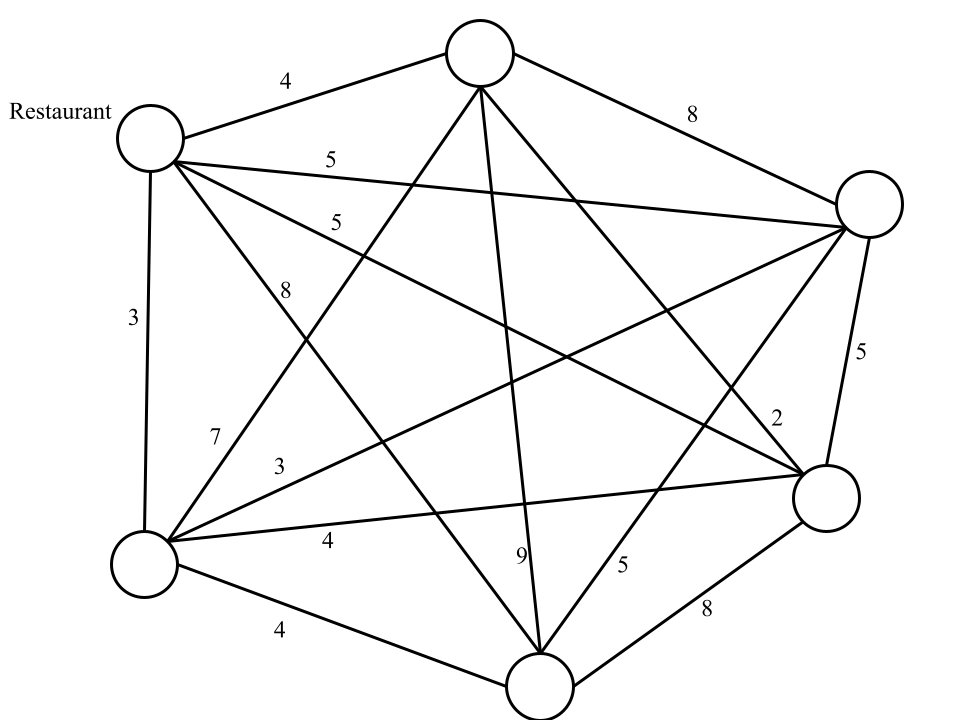
In der Abbildung sind die Stationen und die möglichen Routen als Graph abgebildet. Die Knoten sind die Standorte der Kunden bzw. das Restaurant. Also alle Punkte die der Fahrer abfahren muss. Die Kanten (also die Verbindungen zwischen den Knoten) stellen die Strecken dar, die der Fahrer zwischen zwei Knoten fahren kann. Die Zahlen an den Kanten stellen die Zeit in Minuten dar, die der Fahrer braucht, diese Strecke zu fahren.
Die Aufgabe des Fahrers ist jetzt, eine sogenannte Rundreise zu erledigen. Er startet bei dem Restaurant und muss dort auch wieder am Schluss ankommen. Zwischendrin muss er alle Kunden abfahren. Er darf nie einen Kunden mehrmals besuchen.
Das Problem des Handlungsreisenden ist nun, dass der Fahrer so schnell wie nur möglich seine Rundreise beenden muss. Zeit ist schließlich Geld. Also muss versucht werden, eine Rundreise zu finden, in der die benutzten Strecken so wenig Zeit wie möglich beanspruchen.

Zusammenfassung

Wird eine schnelles Lösungsverfahren für irgendein NP-vollständiges Problem gefunden, dann gilt sofort $P = NP$. Es gab schon einige Beweisversuche für $P = NP$ und auch für $P \neq NP$. Die haben sich jedoch alle als fehlerhaft herausgestellt. Falls irgendwann ein gültiger Beweis für $P = NP$ vom Himmel fällt, wäre der Aufschrei so groß, dass man diesen auch in der Nichtinformatiker-Welt deutlich wahrnehmen würde. Große Probleme wie zum Beispiel in der Medizin wären gelöst, Online-Banking wäre plötzlich abgeschalten und meine Lieferando-Pizza würde schneller ankommen.