Im zweiten Teil von Wer nicht sortiert der länger sucht möchte ich auf den Teil des Suchens eingehen.
Nach dem letzten Teil konnten wir unseren Kartenstapel sortieren, jetzt wollen wir mal sehen welchen Vorteil uns das gebracht hat.

Achtung: Wie in den anderen Teilen der Serie werde ich auch hier in einigen Teilen stark vereinfachen. Dieser Text soll vor allem neugierig machen und nicht terminologisch 100% korrekt sein.

Lass uns (nochmal) ein Spiel spielen

Dieses mal ist es das Ziel eine bestimmte Karte in einem Kartenstapel zu finden. Wenn wir das bei einem unsortierten Kartenstapel machen ist klar, dass wir im schlimmsten Fall alle Karten durchsuchen müssen. Versuchen wir das wieder in der O-Notation auszudrücken. Bei einem Kartenstapel mit n Karten, hat die Suche nach einer bestimmten Karte also die Laufzeit von $\mathcal{O}(n)$ (Zur Erinnerung: n steht hier für eine beliebig große Zahl). Dieser Algorithmus hat auch einen Namen: Lineare-Suche. Für unsortierte Kartenstapel ist dieses Vorgehen oft die einzige Möglichkeit.

Das geht besser

Dass das besser geht sollte klar sein. Wir haben nämlich einen Vorteil, wir bekommen einen sortierten Kartenstapel. Was wir nun machen können nennt sich Binäre Suche. Bei der Binären Suche wird die mittlere Karte im Kartenstapel angesehen. Ist diese Karte größer als der gesuchte Wert, weiß man, dass die gesuchte Karte vor der mittleren Karte liegen muss. Ist die mittlere Karte kleiner, so liegt die gesuchte Karte dahinter. Man hat nun also den Kartenstapel geteilt. Ein Stapel enthält die gesuchte Karte, der andere unter Garantie nicht.
Den Stapel bei der die Karte nicht ist, kann jetzt “weggeworfen” werden. Nun wiederholen wir das ganze mit dem übrig gebliebenen Stapel so lange bis wir nur noch die gesuchte Karte vor uns liegen haben.
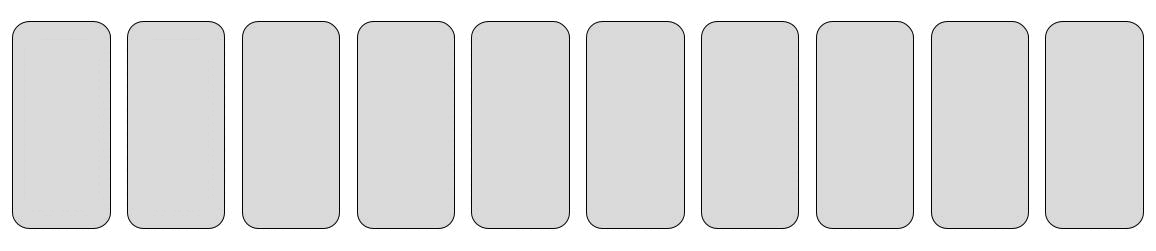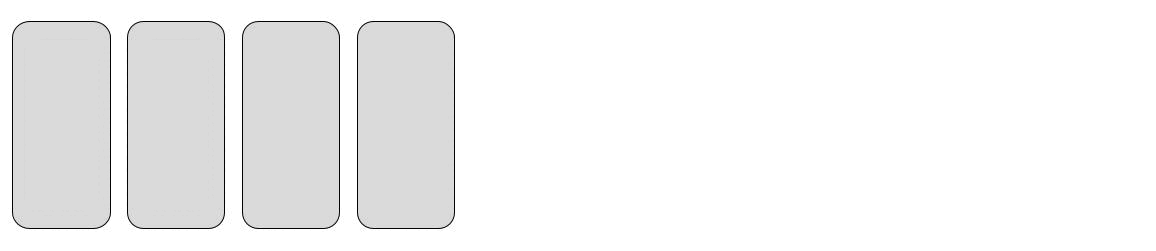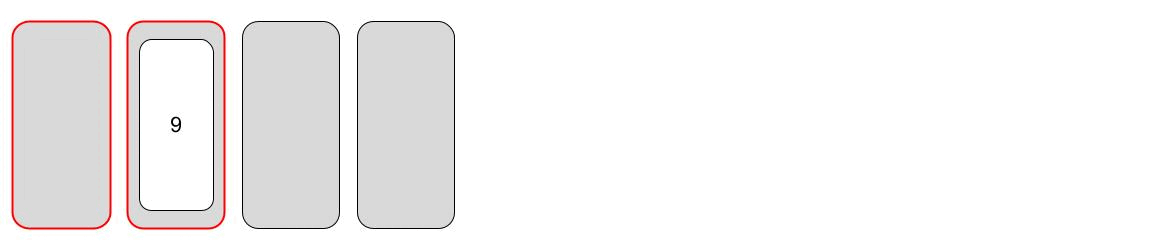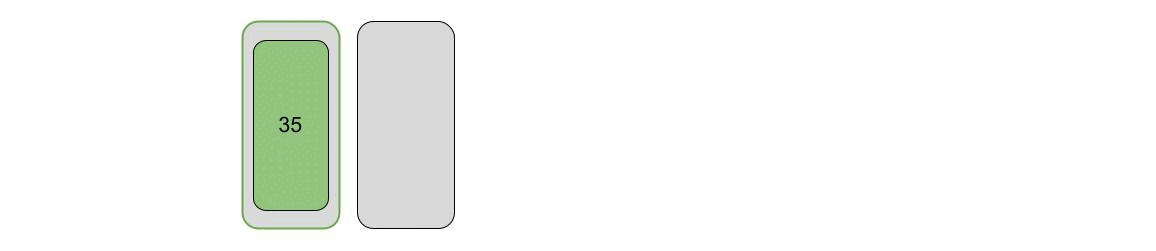In der Beispiel Animation wird die Karte 35 gesucht.

Wie schnell war das jetzt? Versuchen wir das ganze wieder in die O-Notation zu bringen. Dazu müssen wir uns fragen, welche Arbeit machen wir bei dem Algorithmus eigentlich. Und wenn ja, wie viel Arbeit? Im schlechtesten Fall halbieren wir den Kartenstapel so lange bis wir nur noch eine Karte übrig haben. Die Frage die wir also beantworten wollen ist: Wie oft kann ich einen Kartenstapel mit n Karten halbieren.
Das ist gar nicht so trivial zu verstehen, deshalb formuliere ich die Frage um: Wie oft kann ich eine Karte verdoppeln bis ich n Karten habe.
Ich drehe somit die Frage um. Die Antwort ist bei beiden Fragen identisch. Wenn wir die zweite Frage nun in eine Formel gießen müssten wäre diese $n = 2^x$. x ist hierbei die Antwort auf unsere Frage. Die Formel würde in Worten lauten: Wie oft muss ich 2mal2 rechnen, bis ich zu n komme. Da wir n schon wissen wollen wir die Formel nun auf x umstellen. Also $\log{n} = x$. Das bedeutet, alles zusammengefasst, wir können unseren Kartenstapel maximal $\log{n}$ mal halbieren bis wir nur noch eine Karte vor uns haben.
Für unsere O-Notation heißt das also, dass die Binäre Suche eine Worst-Case-Komplexität von $\mathcal{O}(\log{n})$ besitzt.
Übrigens in der der Informatik bedeutet $\log$ eigentlich immer $\log_2{}$, wir sind nur zu faul das ganze auszuschreiben. Lieber stiften wir etwas Verwirrung. Um das ganze mal in Relation zu setzten. Stellen wir uns einen Kartenstapel mit 1000 Karten (in Worten eintausend) vor. Wir müssen beim Suchen nur maximal $\log{1000}$ also 10 Karten ansehen. Das ist wirklich ein großer Vorteil gegenüber unserem ersten Verfahren (Dort hätten wir im schlechtesten Fall alle 1000 Karten ansehen müssen).
Aber Vorsicht: Wenn wir erst die 1000 Karten sortieren, nur um danach eine Karte zu suchen, dann sind wir mit dem ersten Verfahren schneller. Das Sortieren lohnt sich erst, wenn wir mehrere Karten aus demselben Kartenstapel suchen.

Teile und Herrsche

Noch ein Wort zu der Binären Suche. Der Algorithmus funktioniert nach dem “Teile-und-herrsche” Prinzip. Dabei wird ein großes Problem so lange in kleine Teilprobleme zerteilt, bis die Lösung (fast) trivial ist. Wenn man kurz darüber nachdenkt wird klar, wie dieses Prinzip bei der Binären Suche angewandt wird. Unser Stapel wird so lange verkleinert, bis wir die Lösung vor der Nase liegen haben.

Ausblick

Es gibt noch eine Menge anderer Suchverfahren. Die werden in erster Linie dann interessant, wenn der vorhandene Kartenstapel nur teilweise sortiert ist.
Hier zu erwähnen ist das Suchen in Bäumen. Eventuell kommt da nochmal ein Nachtrag ;)

Aber zunächst sollte das mal genug Input sein.

TLDR;

Das Suchen von Daten geht schneller wenn diese vorher sortiert werden. Aber nur, wenn wir diese Daten öfters für eine Suche verwenden.