Im zweiten Teil meiner Serie: “Die Schönheit der Algorithmen und Datenstrukturen” will ich zeigen, wie man mit verschiedenen Algorithmen Karten sortieren kann. Auch will ich zeigen, wie und warum diese Algorithmen, obwohl das Ergebnis das selbe ist, völlig verschieden sind.

Achtung: Wie in den anderen Teilen der Serie werde ich auch hier in einigen Teilen stark vereinfachen. Dieser Text soll vor allem neugierig machen und nicht terminologisch 100% korrekt sein.

Lass uns ein Spiel spielen

Lass uns mal ein neues Spiel erfinden. Jeder Spieler bekommt dafür 10 Karten. Diese Karten haben jeweils eine Zahl von 1-100 drauf. Die Karten liegen dabei verdeckt vor einem auf dem Tisch. Das Ziel des Spieles ist es, seine Karten zu sortieren, und dabei so wenig Züge wie möglich zu benötigen. Ein Zug entspricht dem Ansehen oder dem Bewegen einer Karte. Wer seine Karten sortiert hat und dabei am wenigsten Züge gemacht hat, gewinnt.
Die Frage die man sich nun als Spieler stellt: Wie sortiere ich meine Karten so effizient wie möglich?

Dieses Spiel scheint zwar sehr gestellt (ist es ja auch) aber dennoch bildet es eine sehr häufige und komplexe Problemstellung in unserer digitalen Welt ab. Eine Google-Suche würde zum Beispiel ewig dauern, wenn jede einzelne Webseite erst durchsucht werden müsste, nachdem du den Suchbegriff eingegeben hast. Die Stichwörter die man eingibt hat Google bereits sortiert in einer Liste liegen und kann ein Ergebnis deshalb schneller liefer, als wenn die ganze Liste erst durchsucht werden müsste.
Das selbe Problem gibt es auch in der analogen Welt. Stell dir mal ein Telefonbuch vor, welches keine Sortierung hat. Da wäre das Telefon schnell ausgestorben.

Ein erster Ansatz

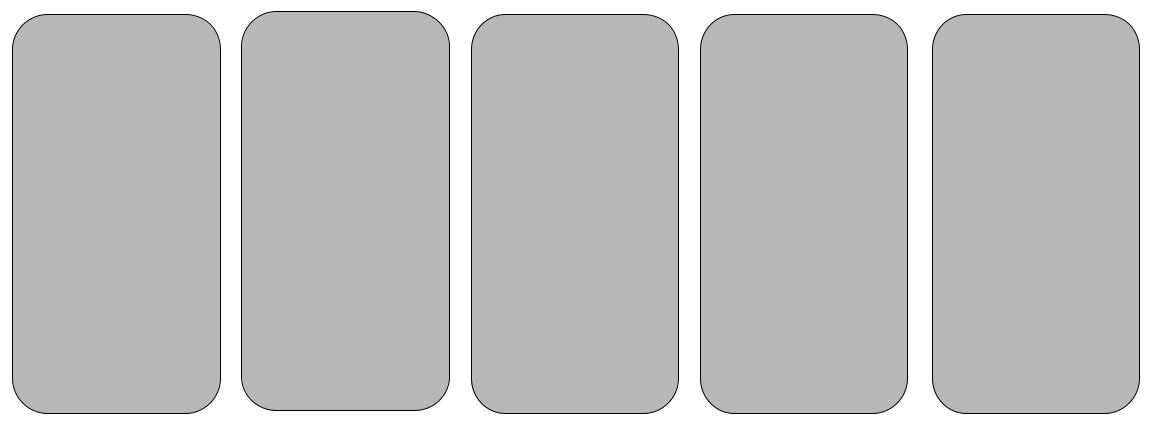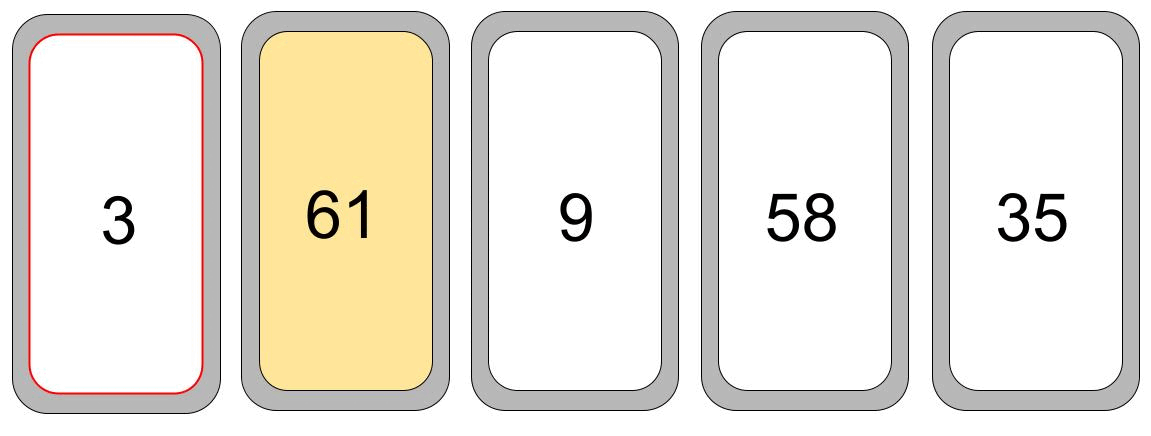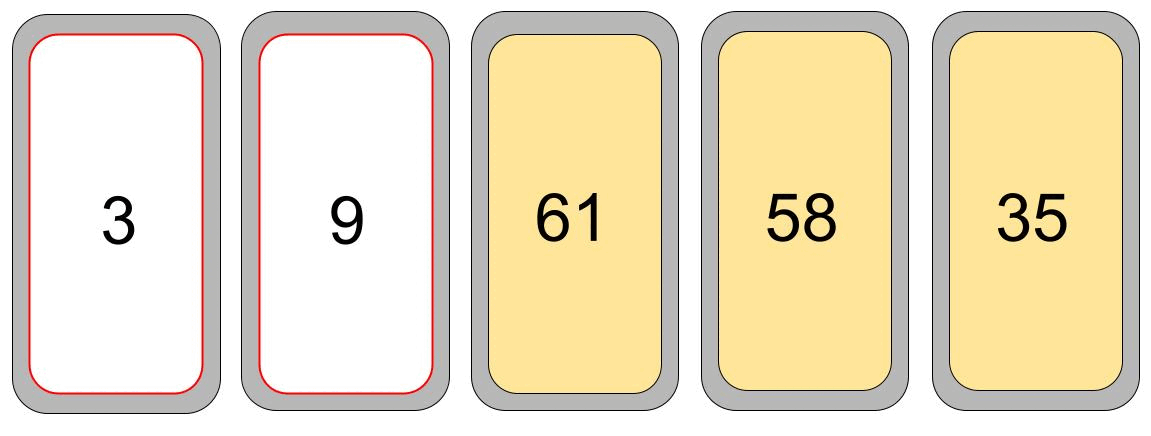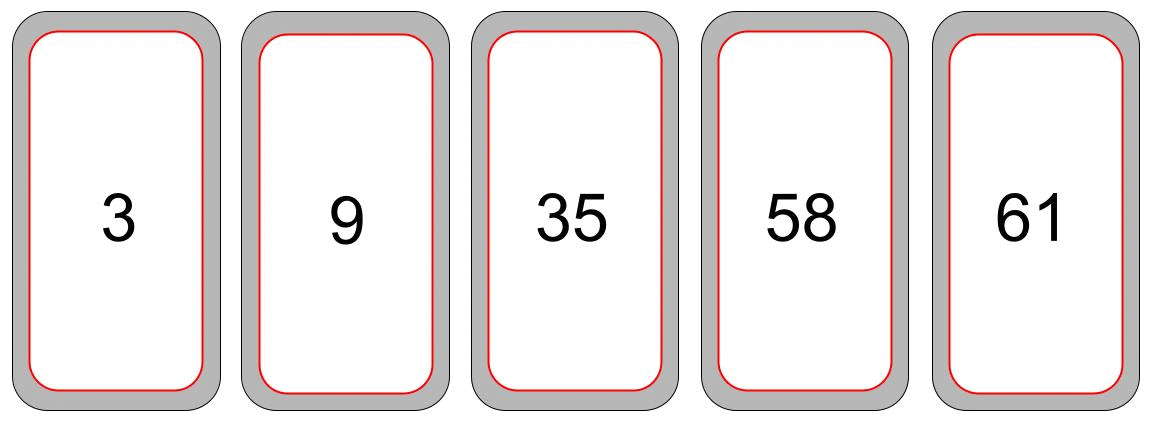
Zurück zu unserem Spiel. Stellen wir uns zunächst mal dumm und sortieren die Karten nach dem ersten Prinzip welches uns in den Sinn kommt. Leg gerne mal eine kurze Lesepause ein und überlege wie du die Karten sortieren würdest. Nun gut, am einfachsten ist es, die Kartenreihe nach der kleinsten Zahl zu durchsuchen, und diese dann ganz links abzulegen. Danach fangen wir wieder von vorne an, aber nun suchen wir das Minimum ab der zweiten Karte. Dieses Verfahren wenden wir so lange an, bis wir bei der letzten Karte angekommen sind und so alle Karten sortiert haben. Ich habe versucht dieses Vorgehen (Algorithmus) in einer kleinen Animation darzustellen. Ein (eindeutig) sehr primitiver Algorithmus. Er wird auch Selection-Sort genannt.
Wie viele Züge brauchen wir im schlechtesten Fall um die Karten zu sortieren? Nun ja, im ersten Durchgang müssen wir alle 10 Karten ansehen, im zweiten Durchgang nur noch 9, im dritten nur noch 8 usw. Also 10 + 9 + 8 … + 1, das ergibt insgesamt 55 Züge. Lass uns das mal für einen etwas allgemeineren Fall betrachten. Nehmen wir mal an, wir haben n Karten (also eine beliebige Anzahl). Die Anzahl der Züge ist dementsprechend n + (n-1) + (n-2) + ... (n-(n-1)). Evtl. kommt dir das aus der Schule bekannt vor, dass ist die gaußsche Summenformel. Das bedeutet für den allgemeinen Fall mit n Karten, benötigen wir $\frac{n^2 + n}{2}$ Züge um n Karten zu sortieren.

O-Kalkül

Ohne es zu wissen haben wir hier schon eine wichtige Analyse des Algorithmus durchgeführt. Die sogenannte Worst-Case Analyse. Das Ergebnis der Analyse wird oft auch im O-Kalkül geschrieben. Das O-Kalkül betrachtet nur das Wachstum eines Algorithmus, also wie viele Züge braucht man mehr, wenn man mehr Karten hinzufügt. Das schöne am O-Kalkül ist, das man nur den Teil betrachtet, der das größte Wachstum ausmacht. In unserem Fall wird also $O(\frac{n^2 + n}{2})$ zu $O(n^2)$.
Das O-Kalkül ist ein wichtiges Werkzeug in der Informatik. Es gibt uns eine Möglichkeit, wie wir Algorithmen miteinander vergleichen können. Würden wir nun einen Algorithmus finden, der eine Worst-Case Laufzeit von $O(n)$ hätte, sollten wir natürlich diesen bevorzugen um das Spiel zu gewinnen.

Geht es noch schneller? Ja!

Wie bereits gesagt ist der Selection-Sort Algorithmus nicht besonders schnell. Jedoch ist er sehr einfach zu verstehen.
Ein sehr schneller Algorithmus ist das Heap-Sort Verfahren.
Um den Heap-Sort Algorithmus zu verstehen, müssen wir uns zunächst ein paar Eigenschaften genauer ansehen und neue Begriffe klären.

Was ist ein Heap

Ein Heap ist zuerst einmal eine Datenstruktur, also ein Gedankengebilde bzw. ein Objekt in dem Daten organisiert sind.
Diese Datenstruktur ist wie ein Baum aufgebaut. Nun muss man wissen das wir Informatiker selten vor die Türe gehen und nur überliefert bekommen, wie Bäume auszusehen haben. Irgendwo in dieser Überlieferung muss sich wohl ein Fehler eingeschlichen haben. Bäume in der Informatik schauen nämlich so aus. Ich glaube man sieht das Problem ganz gut. Die Blätter sind unten und die Wurzel ist oben.
Ein Heap sieht ähnlich aus. 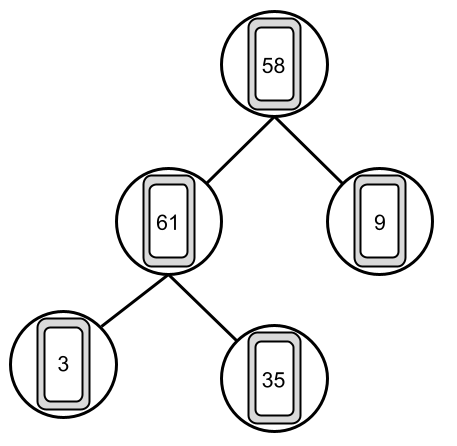Die Karten werden hier in einer Struktur abgebildet die dem vorherigem Baum ähnlich ist. Ganz oben, hier die 58, haben wir die Wurzel. Die Karten in der letzten Reihe 3, 35, 9 werden Blätter genannt. Die Karten liegen jedoch weiterhin in einer Reihe auf dem Tisch, also in der Reihenfolge 58, 61, 9, 3 und 35. Der Baum wird also von oben nach unten und von links und rechts gelesen.
Der Baum der hier abgebildet ist, ist ein Binär-Baum, das heißt, dass ein Knoten (Kreis) sich immer in maximal zwei andere Knoten aufspaltet.
Was wir nun für den Heap-Sort Algorithmus brauchen ist ein binärer Min-Heap. Ein Min-Heap hat zusätzlich die Eigenschaft, dass der Wert eines beliebigen Knotens immer kleiner ist, als alle Werte unter ihm. Das heißt gleichzeitig, dass das Minimum immer in der Wurzel steht. 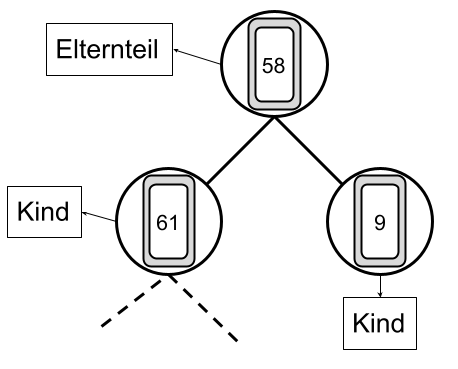Noch kurz zu den Begrifflichkeiten, jedes Element in einem Baum (bis auf die Wurzel) ist ein Kind eines anderes Elements. Bei einem Binär-Baum hat jedes Elternteil (wie man sich bereits denken kann) maximal zwei Kinder. Die meisten Kinder (alle bis auf die Blätter) sind gleichzeitig Elternteile ihrer Kinder. Man kann sich das ganze also vorstellen wie ein Stammbaum einer großen Familie. Jedes Elternteil stellt zusammen mit seinen Kindern einen Teilbaum dar. Eine weitere Eigenschaft des Baumes ist seine Höhe. Sie ist definiert durch den längsten Pfad von der Wurzel bis zu dem entferntesten Blatt (oder anders ausgedrückt: Die Anzahl der Ebenen im Baum). Im Falle des vorletzten Bild, hat der Baum eine Höhe von drei.

Heapify

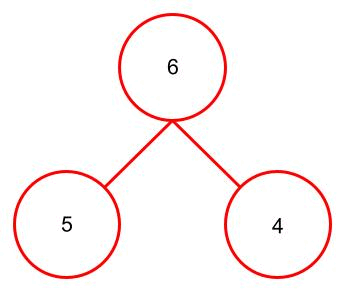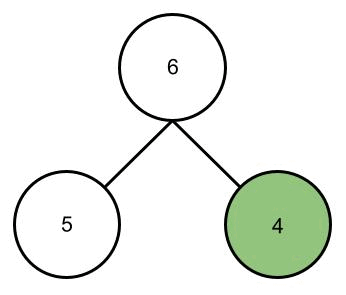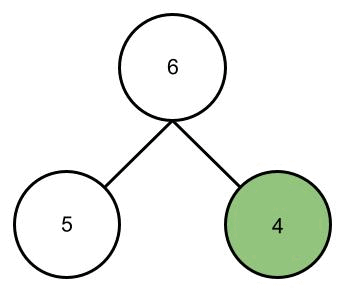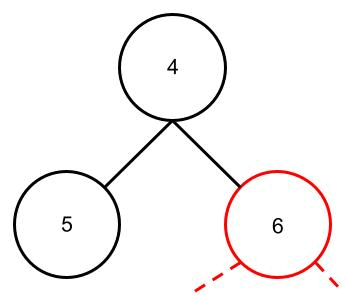
Um aus einem beliebigen Binär-Baum einen Min-Heap zu bauen, müssen wir das Heapify Verfahren anwenden. Aber, wie bei fast allem im Leben, um etwas anwenden zu können, muss man es erst verstehen. Was ist bzw. macht also das Heapify Verfahren. Man nimmt sich für das Heapify-Verfahren immer ein Elternteil mit seinen Kindern vor (also ein Teilbaum). Zunächst wird das Minimum der beiden Kinder ermittelt. Dabei wird das kleinste Kind (also das Minimum) mit dem Elternteil verglichen. Sollte das kleinste Kind kleiner als das Elternteil sein, tauschen die beiden die Plätze. Falls Plätze getauscht worden sind, wird das Verfahren auf den nächsten Teilbaum angewendet bei dem das kleinste Kind das Elternteil ist (das nennt man nebenbei Rekursion). Ich habe versucht das Verfahren in der folgenden Animation zu veranschaulichen.

Erstellen des Heaps

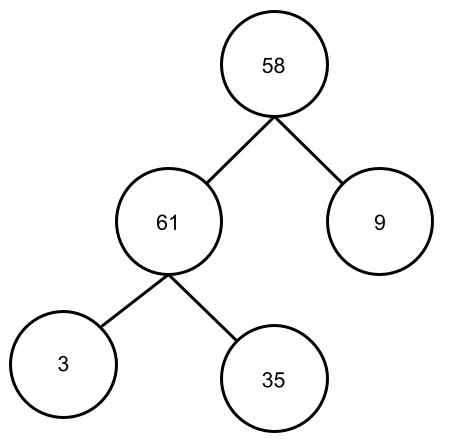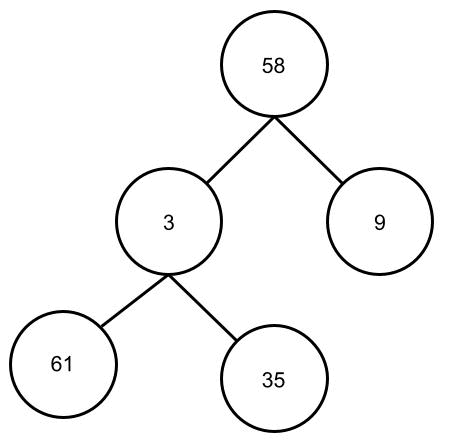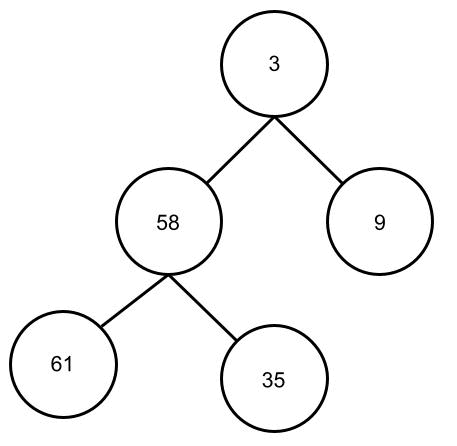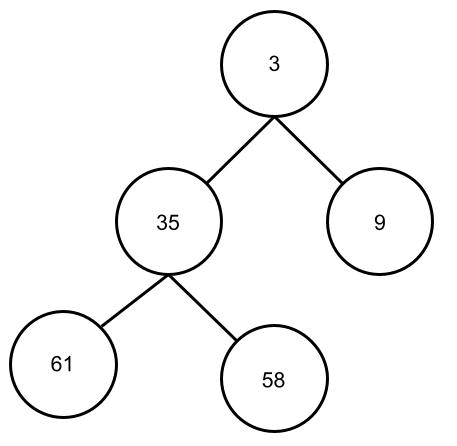
Um nun unsere Karten durch den Heapsort-Algorithmus sortieren zu lassen, müssen wir erst aus unserem Binär-Baum einen Min-Heap erstellen. Dazu wenden wir das Heapify-Verfahren für jedes Elternteil des Baumes an. Also für alle Elemente bis auf die Blätter. Bei unserem Binär-Baum mit den 5 Karten müssen wir das Heapify-Verfahren also zweimal anwenden. Wichtig ist, dass das Verfahren von unten nach oben angewendet wird. Ich hoffe man kann die folgende Animation nachvollziehen. Man kann sehen, wie die kleinen Zahlen nach oben “wandern” und die großen nach unten “durchsickern”.

Heapsort

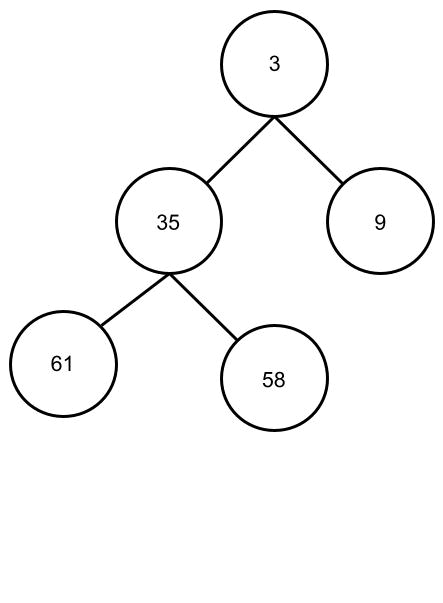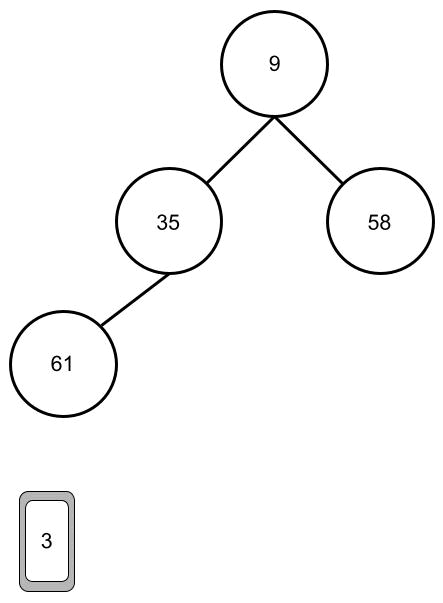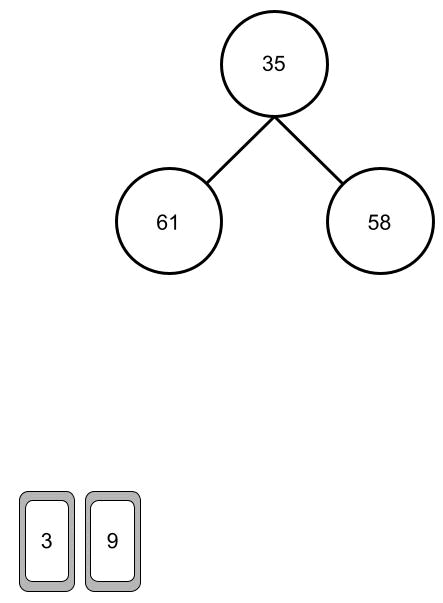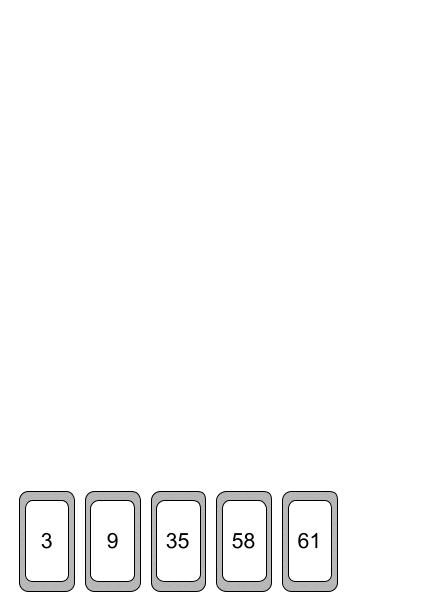
Nachdem der Min-Heap erfolgreich von uns erstellt worden ist, kann der Heapsort angewendet werden. Da wie bereits erwähnt das kleinste Element immer die Wurzel des Heaps ist, kann im Prinzip die Wurzel entfernt und danach der Baum “repariert” werden. Da der Baum nicht ohne Wurzel existieren kann, entfernen wir die Wurzel nicht, sondern tauschen sie gegen das letzte (am weitesten unten und am weitesten rechts) Element aus. Da nach diesem Tausch nicht mehr das kleinste Element die Wurzel bildet, muss der Heap “repariert” werden. Um den Heap zu reparieren können wir einfach das Heapify-Verfahren an der Wurzel ausführen. Das machen wir so lange, bis wir keine Elemente im Heap mehr haben. In der Animation kannst du sehen, wie der Heap immer kleiner wird und die Karten unten sortiert werden.

Ist das wirklich schneller?

Wenn man die Animation ein paar mal ansieht, fällt einem schon auf, dass nicht mehr jede Zahl mit jeder anderen Zahl verglichen wird, wie es bei unserem ersten Ansatz der Fall war. Das liegt daran, dass wir jetzt die Eigenschaften des Heaps ausnutzen können. Wir wissen ja, dass ein Elternteil immer kleiner als seine Kinder ist.
Stellen wir uns mal eine beliebige Karte vor, wenn wir nun überprüfen wollen, ob diese Karte die kleinste in unserem Kartenstapel ist, reicht es aus, wenn wir nur die Wurzel unseres Heaps ansehen. Da wir ja wissen, das alle anderen Karten größer als die Wurzel sind, ist die Frage schon nach einem Vergleich beantwortet.
Jetzt schauen wir uns den Beweis noch etwas genauer an. Wir nehmen als Hilfsmittel wieder das O-Kalkül. Um das Heapsort-Verfahren anwenden zu können, müssen wir zunächst den Heap erstellen. Das machen wir indem wir Heapify für alle Teilbäume ausführen. Es müssen also zuerst zwei Fragen beantwortet werden. Wie “teuer” ist die Anwendung von Heapify? Wie oft muss Heapify angewandt werden besser oder besser gefragt, wie viele Teilbäume gibt es?

Wie “teuer” ist das Erstellen des Heaps?

Wie “teuer” ist die Anwendung von Heapify?

Lass mich zunächst noch ein mal zusammenfassen was Heapify macht. Heapify stellt sicher, dass das Elternteil immer kleiner ist als seine Kinder. Wir haben festgestellt, dass Heapify rekursiv ausgeführt wird, d.h. es wird so oft ausgeführt, bis die Elemente(Karten) an einer geeigneten Stelle sind. Wie oft kann Heapify also im schlimmsten Fall ausgeführt werden?
Der schlimmste Fall wäre, wenn ein Element an der Wurzel eigentlich am entferntesten Blatt seinen richtigen Platz hätte. Heapify kann pro Durchgang ein Element nur eine Ebene nach unten verschieben. Das bedeutet, dass Heapify so oft ausgeführt wird, wie der Baum hoch ist.
Die Frage ist also, wie hoch kann ein Heap mit n Elementen werden? Ein Heap, oder besser gesagt ein Binär-Baum ist nach dem Verdopplungs-Prinzip aufgebaut. In der ersten Ebene maximal ein Element, in der nächsten zwei, dann vier, acht, ….
Anders ausgedrückt:

• Wenn der Heap 1 Element hat, hat er eine Ebene
• Wenn der Heap 2 bis 3 Elemente hat, gibt es 2 Ebenen
• Wenn der Heap 4 bis 7 Elemente besitzt, hat der Heap 3 Ebenen
• Wenn der Heap 8 bis 15 Elemente besitzt, hat der Heap 4 Ebenen
• …
• Wenn der Heap $2^i$ bis $2^{(i+1)}-1$ Elemente hat, dann hat der Heap i Ebenen

Das zeigt uns, dass wir die Höhe (die Anzahl der Ebenen) schätzen können mit $log_2{n}+1$. Für Heapify bedeutet das, dass die Anwendung von Heapify $O({log_2{n}+1})$ teuer ist.

Wie oft muss Heapify ausgeführt werden um einen Heap zu bauen?

Wie wir bereits festgestellt haben muss Heapify so oft ausgeführt werden wie es Teilbäume gibt. Wie wir bereits beobachten konnten, ist jedes Element (bis auf die Blätter) ein Elternteil eines eigenen Teilbaumes. Das bedeutet, es gibt n - (Anzahl der Blätter) viele Teilbäume. Zur Vereinfachung können wir die Anzahl der Teilbäume mit n abschätzen. Wenn ihr genau wissen wollt, wie viele Blätter man abziehen muss um die genaue Anzahl zu bekommen, könnt ihr euch mal an einem verregneten Samstag-Nachmittag selber nachdenken. Tipp: auch hier hilft das Verdopplungs-Prinzip wieder.

Nun alles zusammen

Nun wieder zurück zum eigentlichen Thema. Wie teuer ist das erstellen des Heaps? Heapify muss für jeden Teilbaum ausgeführt werden. Also Heapify muss n-Mal ausgeführt werden. Also “kostet” uns das Erstellen des Heaps $O(n*(log_2{n}+1))$.

Wie teuer ist das Ausführen von Heapsort?

Jetzt kommt es zum eigentlichen Sortieren. Bei der Anwendung von Heapsort wird die Wurzel so oft entfernt (bzw. ausgetauscht) wie es Elemente gibt. Also n-Mal. Danach wird einmal Heapsort ausgeführt. Also wir tauschen n-Mal die Wurzel aus und führen n-Mal Heapsort aus. Das Austauschen der Wurzel ist primitiv und hat “nur” Kosten 1. Die Kosten für Heapsort haben wir schon im vergangenen Kapitel ermittelt ($O(\log_{2}{n}+1)$ zur Erinnerung). Das Ausführen von Heapsort kostet uns also \(O(n+n*(\log_{2}{n}+1))\) bzw. ausmultipliziert $O(n+n*log_2{n}+n)$.

Nun wirklich ALLES zusammen

Die “komplette” Anwendung von Heapsort umfasst zunächst das Bauen des Heaps und danach die Anwendung des Heapsorts-Algorithmus. Wir fassen also im O-Kalkül die beiden Vorgänge zusammen. Es ergibt sich also \(O(n*(log_2{n}+1) + n+n*log_2{n}+n)\). Da im O-Kalkül nur die Teile eine Rolle spielen, die das Wachstum am meisten beeinflussen, kann der Term noch etwas vereinfacht werden und zwar zu \(O(n*log_2{n})\).
Wenn wir das mit unserem naiven Vorgehen von ganz oben vergleichen, dann fällt uns auf, dass $O(n*log_2{n})$ nicht so schnell wächst als $O(n^2)$. Das Bedeutet, dass der Heapsort Algorithmus, nachweisbar schneller ist.
Vorsicht: Wie vermutlich schon bemerkt, haben wir viel weggekürzt und abgeschätzt. Das Heapsort-Verfahren wird bei 10 Karten nicht schneller sein als bei unserem naiven Ansatz. Auch bei 100 Karten wage ich das noch zu bezweifeln. Aber bei einer Million Karten ist er sicherlich um einiges schneller. Der Heapsort spielt seine Stärken aus, wenn die Anzahl der Karten hoch ist. Und in der digitalen Welt sind große Datenmengen keine Seltenheit. Der naive Algorithmus wird deshalb (hoffentlich) nie verwendet werden.

TLDR;

Was solltest du aus diesem doch etwas langen und anstrengend zu lesenden Kapitel mitnehmen. Auch wenn zwei Algorithmen das selbe tun, können sie doch sehr unterschiedlich sein. Es ist eine Kunst für sich einen passenden Algorithmus zu finden, der schnell ist. Mit dem O-Kalkül haben wir ein praktisches Werkzeug womit wir Algorithmen miteinander vergleichen können. Zu guter Letzt: Informatiker haben keine Ahnung wie Bäume aussehen!