In diesem Artikel werde ich versuchen euch ein paar Taktiken zu erklären, die ein Computer anwendet um euch in einem Brettspiel zu besiegen.
Es war eher ein ruhiger Abend in der WG, als eine Freundin (fast schon aus dem nichts) ein 4-Gewinnt-Spiel aus ihrer Handtasche zog.
Als wir ein paar Runden gespielt haben wurde mir eines klar: Ich war richtig schlecht darin. Und damit meine ich nicht, dass ich ein paar Spiele verloren habe, nein, ich habe, soweit ich noch weiß, kein einziges gewonnen. Nach dieser Niederlage gab es logischerweise nur eine handvoll von Optionen: Aus der WG ausziehen und irgendwo ein neues Leben anfangen, ein paar Stunden hinsetzen und eine Taktik für 4-Gewinnt aneignen, oder ein paar Wochen/Monate hinsetzten und einen Algorithmus entwickeln, der jeden Profi in 4-Gewinnt schlägt.
Klar, dass man sich als Informatiker für die letzte Variante entscheidet. Wobei die erste Variante auch sehr verlockend war.

Noch eine Anmerkungen an die Leute die jetzt behaupten: “Nur weil du das Programm geschrieben hast, dass einen Spieler besiegt, hast du doch nicht den Spieler geschlagen”. Ich würde behaupten, dass diese Beziehung hier transitiv ist. Also ja, wenn mein Programm den Spieler schlägt, habe ich den Spieler geschlagen.

Einleitung

Kurz zur Wiederholung: Wie spielt man 4-Gewinnt?

Hier abgebildet ist ein handelsübliches 4-Gewinnt-Spiel. Ein blaues Brett und gelbe bzw. rote Spielsteine. Das Brett ist 6 Felder hoch und 7 breit. Das Brett hat oben Öffnungen, sodass Spielsteine hineingeworfen werden können. Das Spiel wird mit zwei Spieler gespielt. Ein Spieler bekommt die roten, der andere die gelben Spielsteine.
Im Spielverlauf werfen die Spieler abwechselnd ihre Steine in das Brett. Gewonnen hat der Spieler, der als Erstes vier seiner eigenen Spielsteine in eine Linie bringt. Die Linie darf dabei nicht von anderen Steinen unterbrochen sein. Es ist jedoch egal, ob die Linie horizontal, vertikal oder schräg verläuft.
Es kann jedoch auch passieren, dass kein Spieler gewinnt und das Brett bereits voll mit Spielsteinen besetzt ist. Ein klassisches Unentschieden also.

Ein bisschen Mathematik

Um nun dem Computer das Spielen beizubringen, müssen wir uns erst mal die Informationen ansehen, die wir haben. Anschließend alle unnötigen Informationen wegstreichen und die übrigen schön aufbereiten.
Was habe wir also?

Ein Spielbrett mit einigen oder keinen (am Anfang) Spielsteinen darin. Einen Haufen roter Steine und einen Haufen gelber Steine.
Ist es wichtig zu wissen, wie viele roter bzw. gelber Spielsteine noch übrig sind? Nein, denn wir wissen, dass in einem ordentlichen Spiel soviel Steine vorhanden sind, dass wir ein Unentschieden Spielen können. Das bedeutet, dass wir immer einen Spielstein zur Hand haben, wenn ein Zug möglich ist.
Jetzt haben wir also nur noch das Spielbrett mitsamt den Steinen darin. Diese Informationen können wir als Zustand \(S_i\) bezeichnen. Hier steht i für die Anzahl der bisher getätigten Züge, bzw. genauer gesagt, die Anzahl der Zustände die es vor dem momentanen Zustand gab.
Ein Beispiel: der erste Zustand ist \(S_0\), das leere Brett, kein Stein wurde bis jetzt hineingeworfen. Wenn der erste Spieler einen Stein hineinwirft, ändert sich der Zustand des Spiels von \(S_0\) zu \(S_1\).
Wie viele Zustände kann es in einem Spiel maximal geben? Es können ja maximal soviele Züge getätigt werden, wie das Spielbrett Felder hat. Also 7x6. Zustand \(S_{42}\) ist somit auf jeden Fall ein letzter Zustand, oder auch Endzustand genannt.
Die nächste Frage ist, wie können wir unsere Zustände schön darstellen. Da wir Informatiker auch einen leichten Hang zur Mathematik haben, möchte ich das Spielbrett jetzt erst mal in die Zahlenwelt holen. Da das Spielbett ja bereits wie eine Matrix aussieht, werden wir auch eine solche zur Darstellung verwenden. Wir werden mit der Matrix nicht rechnen, aber es macht die Darstellungen der Spielzustände leichter.
Die leeren Felder werden durch die 0 repräsentiert. Die Spielsteine des Computers werden mit einer 1 und die Steine des Gegners werden mit einer 2 dargestellt. Wenn wir die Spielsituation im obigen Bild in der Matrixschreibweise darstellen, sieht das so aus:

\[\begin{bmatrix} 0 &0 &0 &0 &0 &0 &0 \\ 0 &0 &0 &2 &0 &0 &0 \\ 1 &1 &2 &1 &2 &1 &1 \\ 2 &2 &1 &1 &1 &2 &1 \\ 2 &1 &1 &2 &2 &1 &2 \\ 2 &2 &2 &1 &1 &1 &2 \end{bmatrix}\]

In diesem Beispiel wird davon ausgegangen, dass der Computer die Farbe rot zugewiesen bekommt und der Gegner die gelben Spielsteine.

Jetzt haben wir also die Informationen, die zur Darstellung einer bestimmten Spielsituation benötigt werden. Aber was soll der Computer damit anfangen?
Er soll anhand einer Spielsituation (oder Spielzustand) eine Aktion auswählen, die für ihn von Vorteil ist.
Kurzgesagt, der Computer soll eine Spalte auswählen, in die er seinen Stein werfen kann.

Da wir gerade von Aktionen gesprochen haben, definiere ich diese kurz. Eine Aktion \(a_i\) ist eine Aktion die auf den Zustand \(S_i\) angewandt wird. Eine Aktion ist in unserem Fall das Einwerfen eines Spielsteines in eine der sieben Öffnungen. Wenn wir also als ersten Wurf (also in Spielzustand \(S_0\)) unseren Spielstein in die mittlere Öffnung werfen, dann ist \(a_0 = 4\).

Wie hängt ein Spielzustand und eine Aktion nun zusammen? Eine Aktion überführt einen Spielzustand immer in den nächsten Spielzustand.

\[S_{i+1} = f(S_i, a_i);\]

Wir haben also eine Funktion \(f\), die uns \(S_{i+1}\) anhand von \(S_i\) und \(a_i\) ausrechnet. Wie die Funktion genau funktioniert ist nicht relevant, aber ich denke, dass jeder der schonmal 4-Gewinnt gespielt hat sich vorstellen kann, wie eine bestimmte Spielsituation nach dem Einwerfen von einem Spielstein in eine beliebige Spalte aussieht. Also nochmal als Zusammenfassung:

\[\begin{bmatrix} 0 &0 &0 &0 &0 &0 &0 \\ 0 &0 &0 &0 &0 &0 &0 \\ 0 &0 &0 &0 &0 &0 &0 \\ 0 &0 &0 &0 &0 &0 &0 \\ 0 &0 &0 &0 &0 &0 &0 \\ 0 &0 &0 &0 &0 &0 &0 \\ \end{bmatrix} \xrightarrow{a_0 = 4} \begin{bmatrix} 0 &0 &0 &0 &0 &0 &0 \\ 0 &0 &0 &0 &0 &0 &0 \\ 0 &0 &0 &0 &0 &0 &0 \\ 0 &0 &0 &0 &0 &0 &0 \\ 0 &0 &0 &0 &0 &0 &0 \\ 0 &0 &0 &1 &0 &0 &0 \\ \end{bmatrix}\]

Wie wählt der Computer einen guten Zug aus?

Was unser Computer jetzt braucht, ist eine Funktion \(g\) die Anhand eines Spielzustandes \(S_i\) eine Aktion \(a_i\) berechnet. Dabei soll die Aktion \(a_i\) dem Computer langfristig einen Vorteil bringen.

Also nochmal sauber aufgeschrieben: $a_i = g(S_i)$

Um zu beurteilen, welche Aktion dem Computer langfristig den größten Vorteil bringt, ahmt der Computer bei den meisten Strategien die menschliche Denkweise nach. Deswegen können wir hier tatsächlich von einer Künstlichen Intelligenz sprechen. Bevor wir uns die verschiedenen Strategien ansehen, wie der Computer die Funktion \(g\) umsetzt, möchte ich noch auf die sogenannte Heuristik Funktion eingehen.

Heuristik Funktion

Die Heuristik Funktion bildet bei den meisten Strategien das Herzstück. Dabei nimmt die Funktion einen Spielzustand und bildet diesen auf ein Skalar ab. Kurzgesagt es bepunktet einen beliebigen Spielzustand, also wie gut oder schlecht dieser Spielzustand für den Computer ist. Ist ein Spielzustand besonders gut, weil wir vier Steine in einer Reihe haben, gibt es z.B. 100 Punkte. Ist der Spielzustand nichts sagend, z.B. weil noch kein Spieler einen Wurf getätigt hat, gibt es z.B. 0 Punkte.
Allgemein gesprochen haben wir hier also eine Funktion $h$ die einen Spielzustand $S_i$ nimmt und uns eine Anzahl von Punkten $p$ zurückgibt: \(h(S_i) = p\)

Wie die Heuristik Funktion genau aufgebaut ist, ist von Spiel zu Spiel unterschiedlich. Oft gibt es für beliebte Brett-Spiele, wie z.B. Schach, bereits vorgefertigte Heuristiken, die man nur noch verwenden muss.
In unserem Vier-Gewinnt Spiel würde z.B. eine Heuristik Sinn machen, die einer 4er Linie von unseren Steinen 100, einer 3er Linie 50 und einer 2er 10 Punkte gibt. Meist steht und fällt eine gute Strategie mit der Heuristik Funktion. Es macht also Sinn diese im Laufe der Zeit nochmal zu überdenken bzw. daran etwas rumzuschrauben.

Naive Strategie

Bei der ersten Strategie handelt es sich um einen sehr naiven Ansatz. Dabei betrachten wir den aktuellen Spielzustand $S_i$ und simulieren jede mögliche Aktion auf diesem Zustand. Wir erhalten also maximal 7 neue unterschiedliche Spielzustände $S_{i+1}$. Ich habe mal versucht das in diesem Bild zu verdeutlichen:

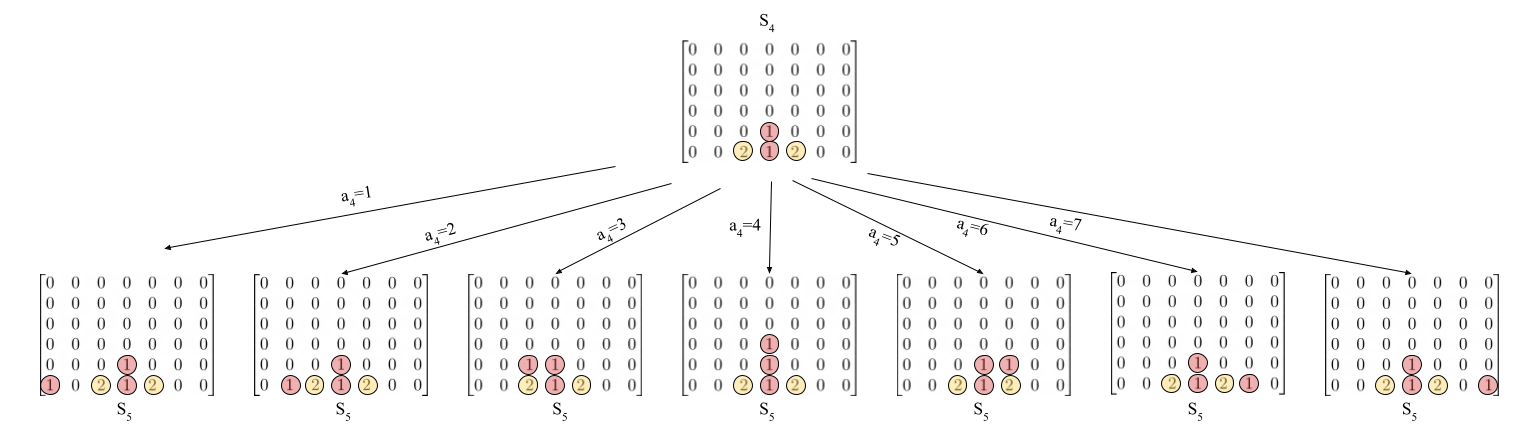
Nun wird für jeden simulierten Zustand die Heuristik Funktion aufgerufen. Danach können wir den Zustand auswählen, der am meisten Punkte bekommen hat. Die Aktion die zu diesem Zustand geführt hat, wird als Aktion für den den nächsten Zug gewählt.
In diesem Beispiel wird vermutlich der mittlere Zustand mit den meisten Punkten bewertet. Die Aktion die deswegen für den Computer ausgewählt wird ist $a_4=4$.

Warum ist diese Strategie nicht besonders gut? Sie ist nur auf einen kurzfristigen Vorteil aus. Genauer gesagt auf den Vorteil im nächsten Zug. Das mag zwar in den meisten Fällen funktionieren, aber oft ist es besser sich etwas aufzubauen um dann zuzuschlagen. Wir müssen also länger in die Zukunft schauen.

Minmax Strategie

Bei der Minmax Strategie wird der Minmax Algorithmus angewandt. Der Minmax-Algorithmus berechnet die Spielzustand ausgehend von dem jetzigen Zustand bis zu einem bestimmten Zeitpunkt. Wie das genau aussieht werden wir uns später noch ansehen. Er ist sogesehen eine Erweiterung der naiven Strategie. Er sieht sich jedoch dabei nicht nur den nächsten Schritt an, sondern sieht z.B. sechs Schritte in die Zukunft. Auch berücksichtigt er dabei alle möglichen Züge des Gegners. Wie das genau aussieht wird im nachfolgenden Bild verdeutlicht. Aus Platzgründen werden in jedem Schritt nur zwei Zustände simuliert. In Wirklichkeit müssten es natürlich 7 sein.

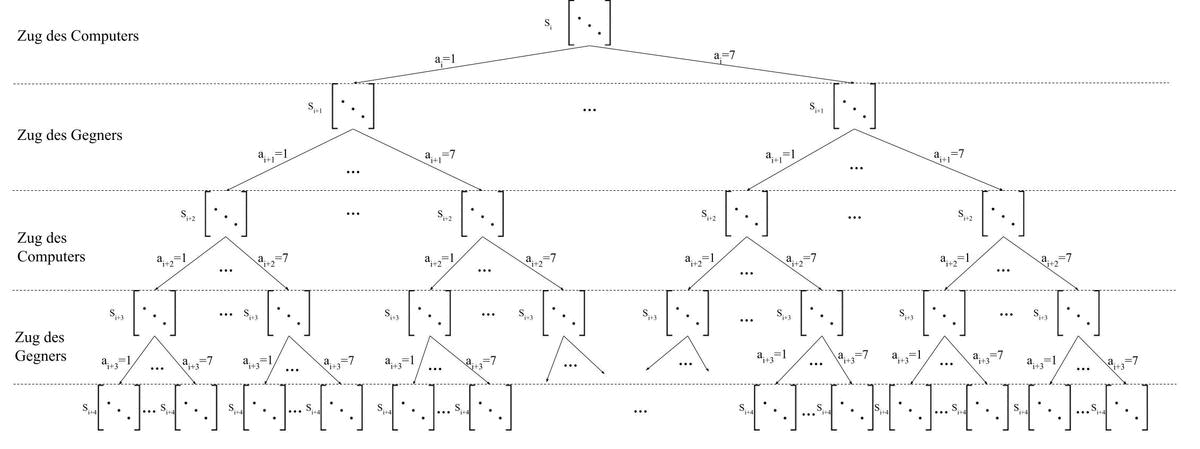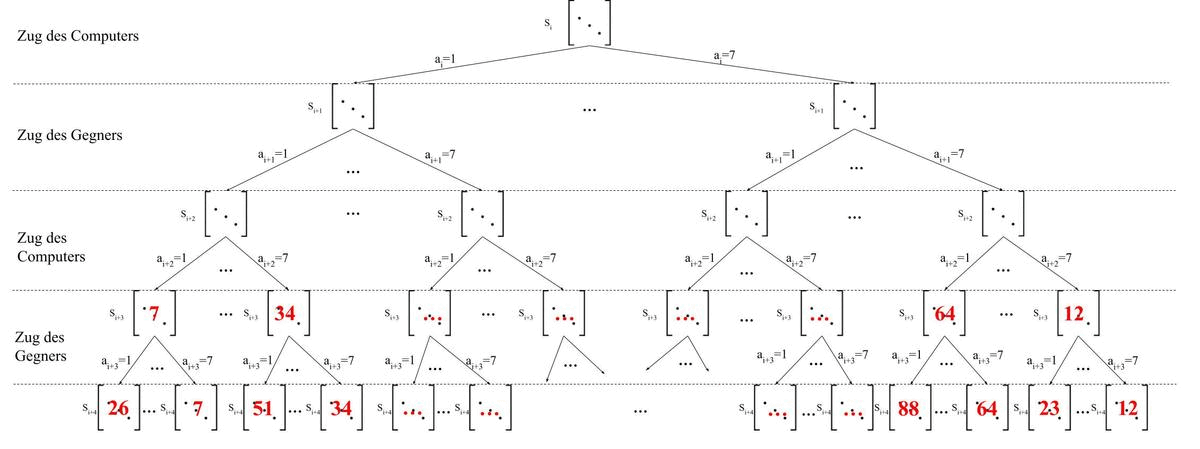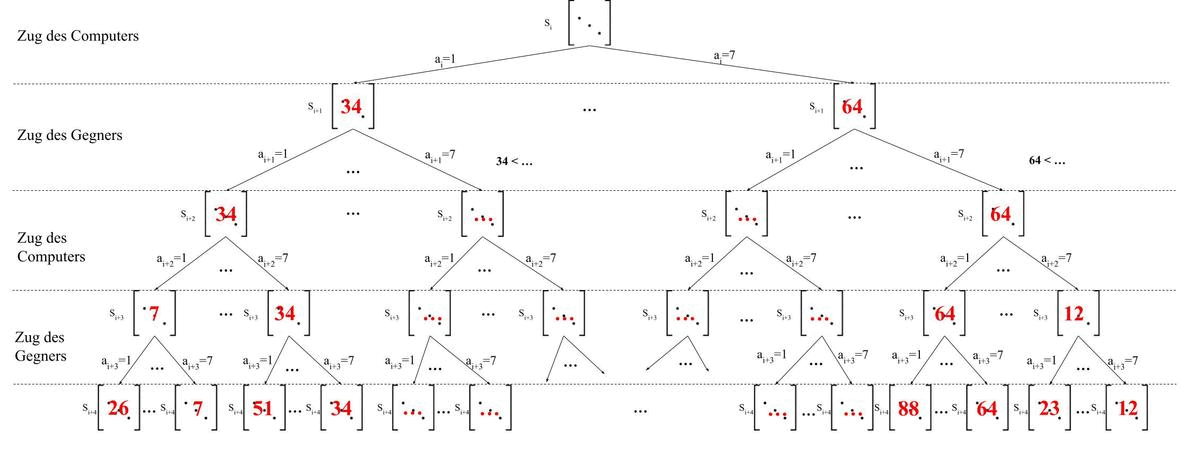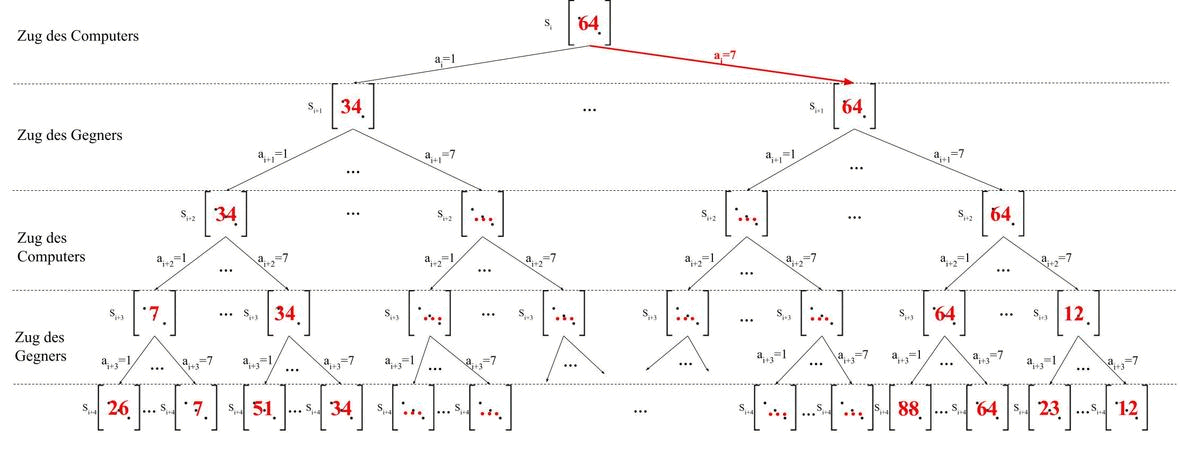
Im nächsten Schritt rufen wir wieder unsere Heuristik Funktion auf. Jedoch nur für die Spielzustände auf der letzten Ebene. Im übrigen werden die Inhalte der letzten Ebene Blätter genannt. Mehr dazu gibt es in einem meiner letzten Artikel. Nun werden die Ebenen von Unten nach Oben durchgegangen. Die Ebenen, die die Züge des Gegners darstellen, wählen die minimalen Punkten aus der Ebene darunter aus. Die Ebenen, die die Züge des Computers darstellen, wählen die maximalen Punkte aus der Ebene darunter aus.
Dieses Verfahren stellt sicher, dass der Computer seine eigenen Punkte maximiert und betrachtet auch den Fall, dass der Gegner versuchen wird, die Punkte des Computers zu minimieren.
Nun wählen wir wieder den Spielzustand aus, der die meisten Punkte bekommt.
Dieser Spielzustand haben wir ja erreicht, in dem wir eine Kette von Aktionen ausgeführt haben. Aus dieser Kette wählen wir nun die erste Aktion aus, als $a_i$, als tatsächliche Aktion die nun im Spiel ausgeführt werden soll.

Wie viele Zustände müssen hier simuliert werden? In der ersten Ebene haben wir unseren Startzustand, das ist der tatsächliche Zustand des Spieles. Danach simulieren wir durch das gedankliche Einwerfen eines Spielsteines in jede Öffnung sieben weitere Spielzustände. Für jeden dieser sieben Zustände werden wieder jeweils 7 weitere Zustände generiert, usw. Wir simulieren also $(7+7*7+7*7*7+…)$ Zustände. Etwas eleganter aufgeschrieben: \(\sum_{i=1}^{n} 7^i\)

In einem Spiel können ja maximal $7*6=42$ Züge aufkommen. Warum simulieren wir also nicht 42 Schritte voraus? So könnten wir ja immer bis zum Ende sehen, um so den wirklich aller besten Zug berechnen zu können.
Die Problematik ist, dass wir $\sum_{i=1}^{42} 7^i$ Zustände simulieren müssten. Das sind laut Wolframalpha 364 Quintilliarden. Wenn wir bedenken, dass ein moderner Rechner ca. 16 Milliarde Byte an Speicher besitzt, haben wir also schon ein großes Speicherproblem. Geschweige denn, dass wir Jahre brauchen würden, um all diese Zustände zu simulieren. Es macht also Sinn eine geringere Simulationsgröße wie z.B. 6 festzulegen.

Der Minmax-Algorithmus kann noch durch z.B. Alpha-Beta Pruning beschleunigt werden, jedoch will ich darauf nicht eingehen, da die Funktionalität die selbe ist.

Der große Nachteil der Minmax-Strategie ist, dass wir nur ein paar Zeitschritte in die Zukunft dadurch schauen können. Wie können wir das also verbessern?

Monte Carlo Tree Search

Monte Carlo ist nicht nur für seine Rennstrecke sondern auch für seine Casinos und somit auch für Glücksspiele bekannt. Auch in Monte Carlo Algorithmen geht es um Glück. Genauer gesagt um Zufallszahlen.

Wie schon vorher beschrieben, wären alle unsere Probleme gelöst, wenn wir alle Spielzüge vorhersagen bzw. durchsuchen könnten. Warum das nicht möglich ist, haben wir gerade geklärt.
Was ist jedoch, wenn wir von diesem riesigen Baum uns nur ein paar vielversprechende Äste ansehen. Wir picken uns also einen Pfad des Spielbaums raus und schauen, ob wir am Ende des Pfades gewinnen oder verlieren. Gewinnen wir, ist dieser Pfad vielversprechend und wir können ihn genauer untersuchen.

Der Algorithmus durchläuft dabei vier Phasen: Selection, Expansion, Simulation und Backpropagation.

Selection

Zunächst wird ein Blatt (also ein Knoten ohne Kinder) gewählt, der am vielversprechendsten ist. Ob ein Knoten vielversprechend ist oder nicht kann durch verschiedene Kriterien bestimmt werden. Meist ist es jedoch ein Verhältnis zwischen der Anzahl der Besuche und der Gewinne an diesen Knoten.

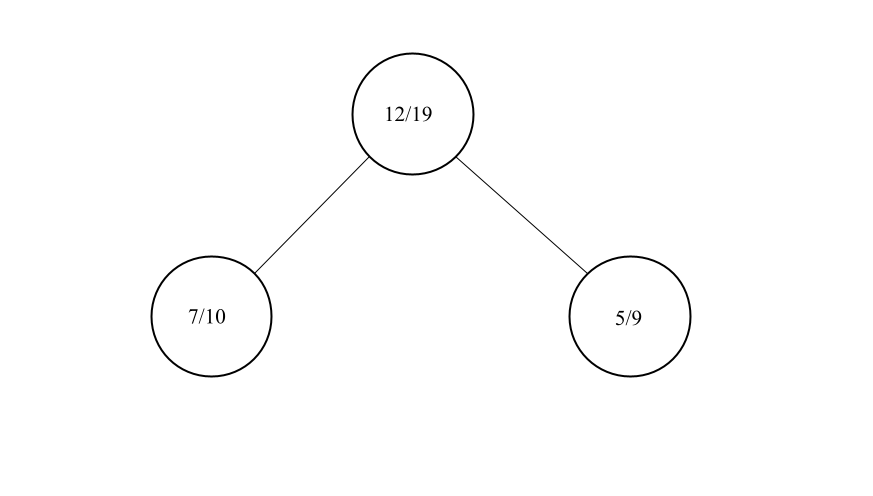
In diesem Bild ist die Beschriftung in den Knoten so zu interpretieren: AnzahlBesuche/AnzahlGewinne. Hier würde der Knoten links unten gewählt werden. Dieser Knoten ist nun Kandidat für die nächste Phase: Expansion

Expansion

Der Knoten der ausgewählt wurde, wird nun expandiert. Das heißt es werden alle möglichen neuen Spielzustände die aus diesem Knoten entstehen können in die nächste Ebene eingefügt.

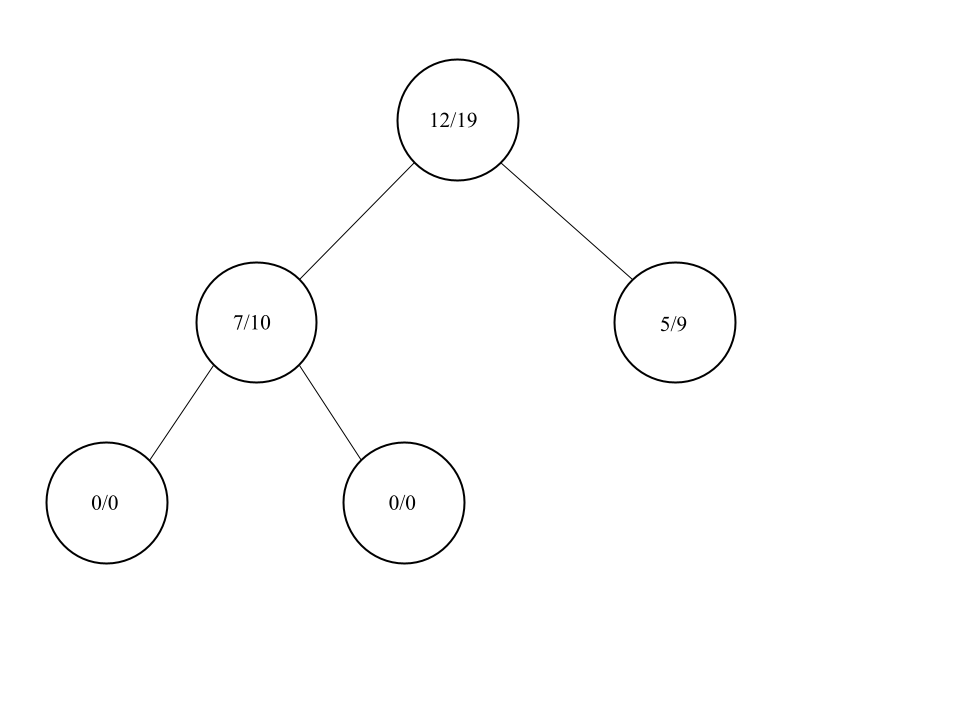
Natürlich müssten es hier wieder sieben neue Knoten sein, jedoch wäre das sehr schnell unübersichtlich. Nun wählen wir aus den neu erstellten Knoten den ersten aus. Dieser wird unser Kandidat für die Simulation.

Simulation

Ab den Spielzustand des ausgewählten Knoten wird nun ein komplettes Spiel simuliert. Dabei wird abwechselnd immer ein Spielzug zufällig gewählt. Am Ende der Simulation haben wir entweder Gewonnen, Verloren oder es ist ein Unentschieden.

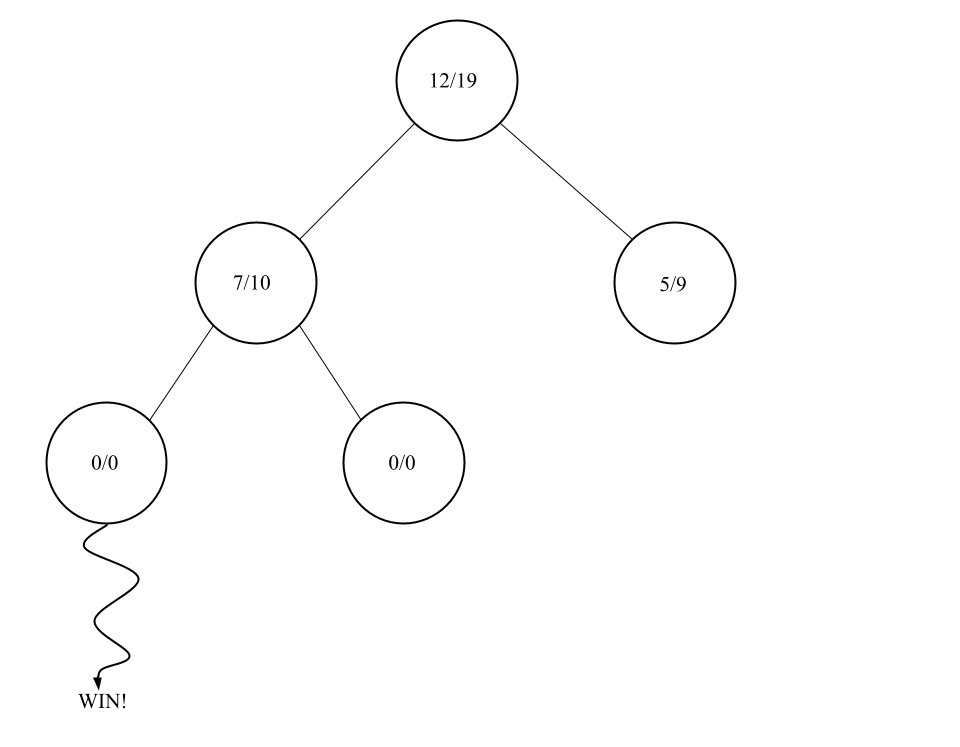
Backpropagation

In der letzten Phase wird das Ergebnis der Simulations-Phase an alle Knoten die direkt darüber sind, weitergegeben. Wenn ein Gewinn entstanden ist, werden die Anzahl der Gewinne um eins erhöht. Außerdem werden noch alle Besucherzahlen um eins erhöht, unabhängig vom Ausgang der Simulation.

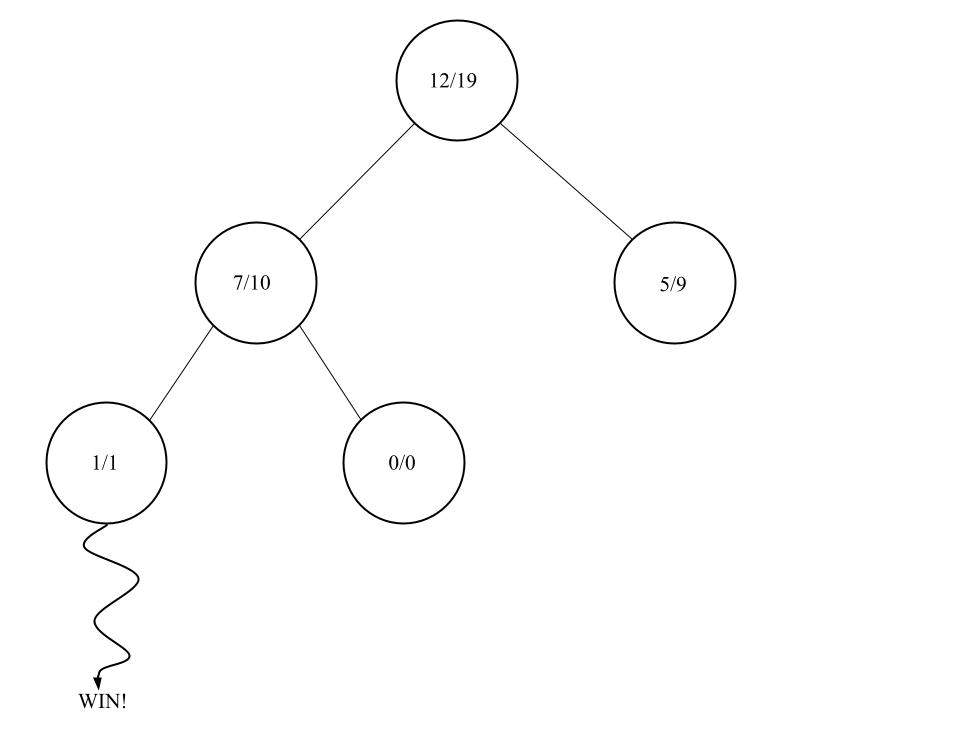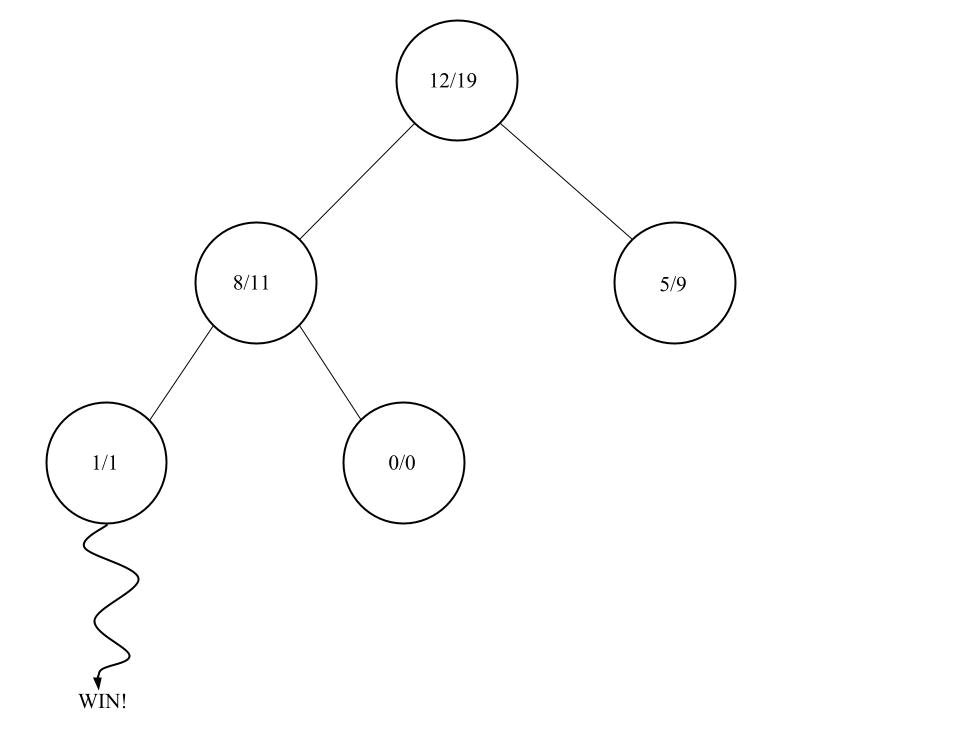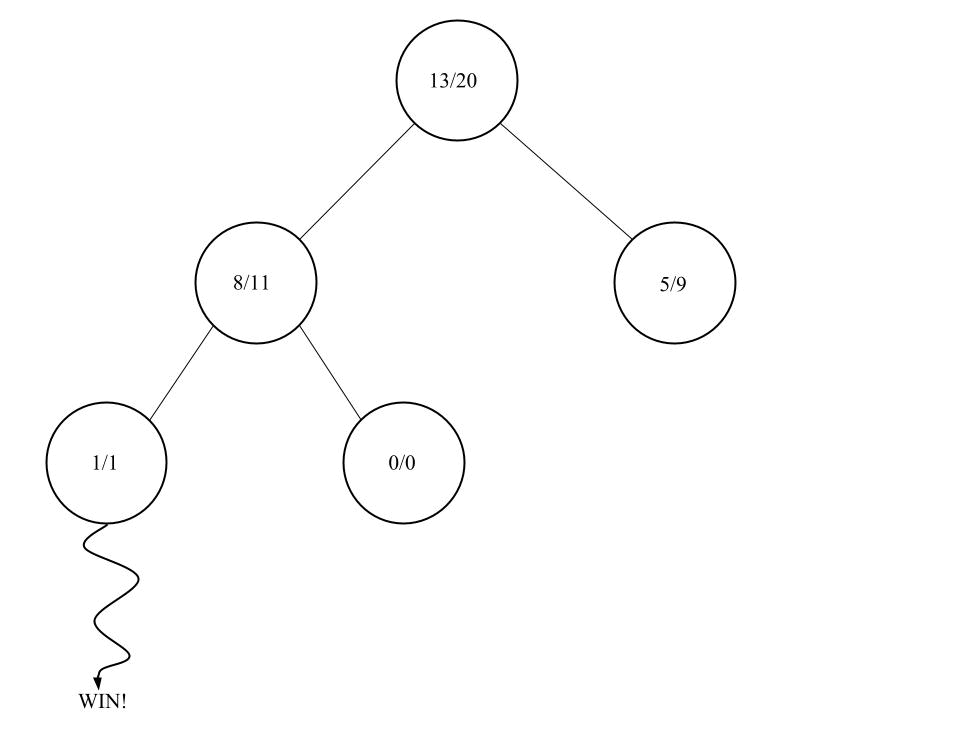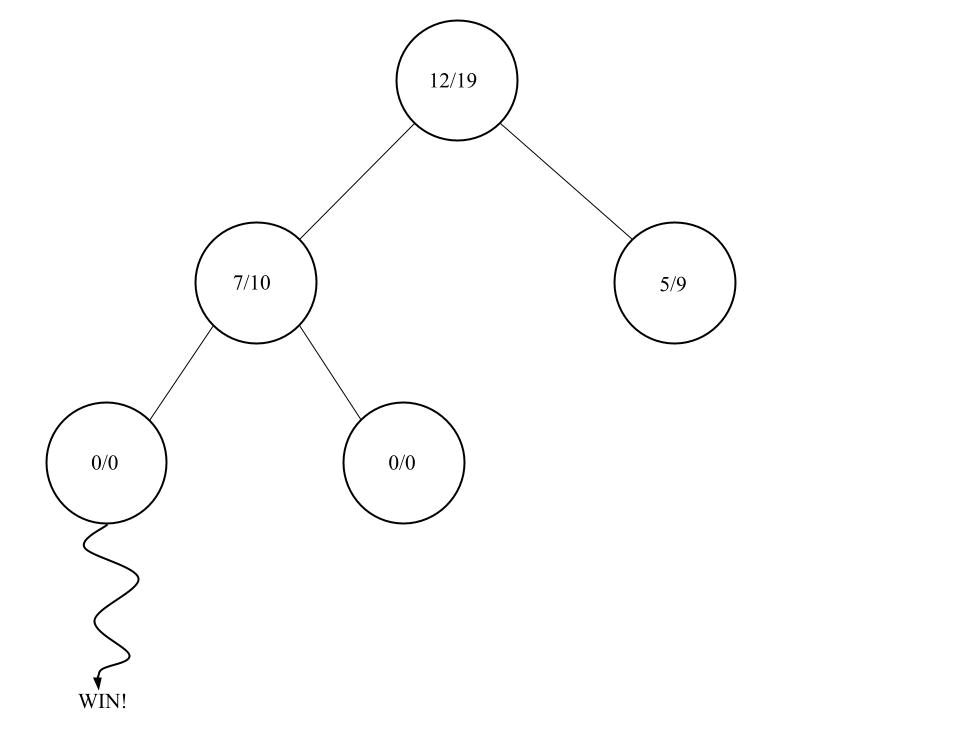
Alle vier Phasen werden jetzt nacheinander ein paar hundert mal wiederholt, bis unser Spielbaum groß genug ist, um eine gewisse Aussagekraft zu besitzen.
Zum Schluss wird der direkte Kindsknoten der Wurzel ausgewählt, der die größte Besucherzahl hat. Die Aktion, die zu diesem Knoten geführt hat, wird wieder als tatsächliche Aktion des Computers ausgewählt.

Der Monte-Carlo-Tree-Search-Algorithmus ist deswegen so interessant, weil er ohne Heuristik Funktion auskommt. Das heißt für uns, wir müssen nicht mehr darauf achten, wie gut unsere gewählte Heuristik Funktion ist. Ist das nicht großartig?
Der Nachteil dieser Methode ist, dass wir Züge übersehen können, da wir ja die Züge zufällig wählen. Diese Gefahr kann jedoch vermindert werden, indem wir die vier Phasen sehr oft wiederholen. Das ist natürlich wieder Rechenaufwendiger. Man muss also einen guten Mittelweg finden.

Aussicht

Das waren jetzt drei KI-Algorithmen, die dem Computer helfen können, dich in Vier-Gewinnt zu schlagen. Ich hätte noch zwei weitere Algorithmen getestet, die auf Machine-Learning basieren. Jedoch werden die erst im nächsten Kapitel besprochen.

Danke fürs lesen, bleibt neugierig